Геометрия 10 класс. Лёгкая задача

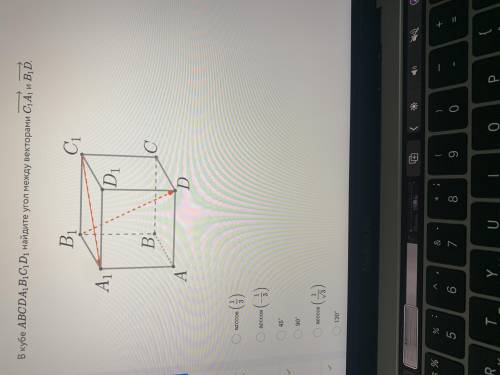
Пусть имеем куб с ребром, равным 1.

Применим простой - перенесём вектор А1С1 в точку В1 и рассмотрим получившийся треугольник EB1D.

Угол EB1D равен углу между заданными векторами.

Отрезок ЕВ1 = А1С1 как диагональ квадрата равен √2.

Диагональ куба B1D равна √3.

Отрезок ED = √(2² + 1²) = √5.

Искомый угол определим по теореме косинусов.

cos(EB1D) = ((√2)² + (√3)² - (√5)²)/(2*√2*√3) = (2+3-5)/(2√6) = 0.

ответ: угол равен arc cos 0 = 90 градусов.