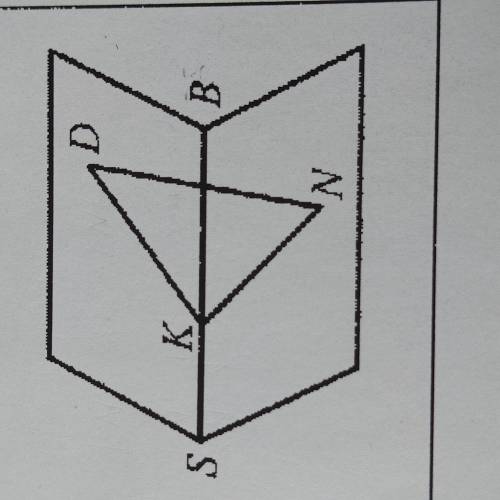
ГЕОМЕТРИЯ 10 КЛАСС ДВУГРАННЫЕ УГЛЫ Дано: KD перпендикулярно SB, KN перпендикулярно SB, KD=KN, угол KDN = 35°
Найти: угол DSBN -?

Чтобы решить эту задачу, давайте рассмотрим имеющиеся данные и пошагово найдем ответ.

Дано:

- KD перпендикулярно SB
- KN перпендикулярно SB
- KD=KN
- угол KDN = 35°

Найти: угол DSBN

Сначала обратим внимание на данные. Мы видим, что наша фигура имеет два перпендикулярных отрезка KD и KN, которые пересекаются в точке K.

Также, мы знаем, что KD=KN. Это означает, что треугольники KDN и KBN равнобедренные, потому что у них равны две стороны KD и KN, и угол между ними, KDN, равен 35°.

Давайте обратимся к треугольнику KDN. У нас есть равнобедренный треугольник с углом KDN, равным 35°. Так как у равнобедренных треугольников основание равностороннего треугольника делится на равные части, у нас будет два равных угла NDK и NDK.

Заметим, что угол NDK и угол SNB являются вертикальными углами и равны между собой, так как они находятся на прямых линиях. Таким образом, угол SNB = 35°.

Осталось найти угол DSBN.

Обратим внимание, что угол DSBN и угол SNB являются вертикальными углами. Поэтому, угол DSBN также равен 35°.

Итак, угол DSBN равен 35°.