ГЕОМЕТРИЯ. 1. Найти полную поверхность конуса, радиус которого 2 см, а высота 7 см (в ответ ввести целую часть без pi)
2. Найти радиус конуса, высота которого 10 см, а образующая составляет угол 30 градусов с плоскостью основания (ответ округлить до сотых -два знака после запятой)
3. Найти площадь осевого сечения конуса, если его высота 8 см, а диаметр 6 см
Другие вопросы по теме Геометрия
Популярные вопросы
- Адам өміріндегі жануарлар әлемі 1 тап Онлайн мектеп көмек точный ответ 5 класс...
1 - Complete the text with the correct form of the verbs in the box. choose | go (×...
3 - Описание рисунка Возвращение ассирийского царя из похода по плану1)Царская колесница2)Унижение...
2 - стихотворения Е.А.Евтушенко Ошеломив меня, мальчишку... , А. С. Кушнера Контрольная....
3 - Наличие веснушек доминантный признак. Девушка с веснушками (гетерозиготная) выходит...
2 - Выпишите все конфликты в произведении Некрасова ,,Железная дорога,,...
1 - 1.Составьте вопросный план к тексту. (5б) 2. Определите основную мысль текста....
2 - Инвидуальный Проект ( ) 1) Определите, какие критерии относятся к реферату? а)...
3 - Сравните слои атмосферы заполнив таблицу...
1 - Составте цитатный рассказ о Хлестакове в комедии Ревизор ....
1
Вроде так)
Объяснение:
1) 6
2) 17,32
3) 24
Объяснение:
№1
Pi буду писать как П
Sп.п.к. = Sб.п.к. + Sосн.
Sб.п.к. = П * R * L
Sосн. = П *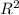
L =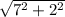 (т.к. треугольник, образованный радиусом, высотой и образующей - прямоугольный) =
(т.к. треугольник, образованный радиусом, высотой и образующей - прямоугольный) = 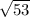
Sб.п.к.= П * 2 *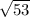 = 2
= 2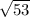 П
П
Sосн. = П *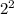 = 4П
= 4П
Sп.п.к. = 2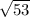 +4 = 6
+4 = 6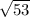
Если нужна целая часть без П, то ответ будет 6, скорее всего
№2
Так как высота перпендикулярна основанию конуса, то высота, радиус и образующая составляют прямоугольный треугольник. Угол равный 30° лежит против катета, равного 10 см. По свойству угла в 30° (угол 30° лежит против катеты, равного половине гипотенузы), гипотенуза = 2*10 = 20 - образующая
По теореме Пифагора найдем радиус
R = =
= 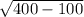 =
= 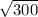
При округлении до сотых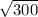 = 17,32
= 17,32
№3
Sо.с.к. = 1/2 * R * H = 1/2 * 8 * 6 = 24