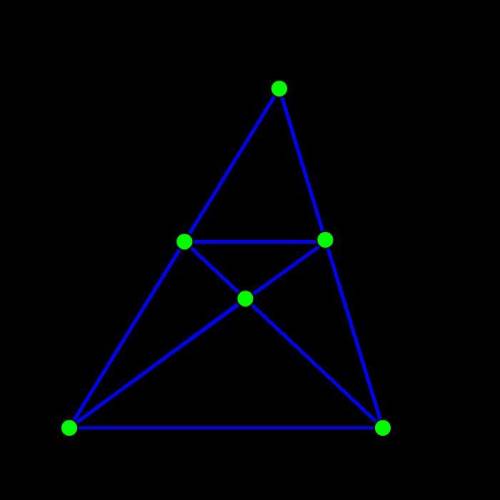
F – точка пересечения AD и BE – медиан треугольника ABC. Известно, что площадь треугольника ABF = 12. Найдите площадь треугольника DEF.
Другие вопросы по теме Геометрия
Популярные вопросы
- Средняя линия трапеции равна 16 см.найдите основания трапеции,если они относятся...
1 - Определите причины образования крупных массовых вечной мерзлоты в евразии...
1 - Сторона ромба равна 15, а диагональ равна 18.найдите площадь ромба...
1 - Написать записку от ученика учительнице, что бы ученик хотел бы предложить...
2 - Образ віконтеси де гранльє .будь ласка напишіть...
3 - Какой из терминов является названием операционной системы? варианты ответов:...
2 - Наземные растения используют 1%энергии солнца. в течение часа 1м квадрате...
1 - Рейка длиной 147см разрезана на 4 ровные части.какую длину имеет каждая...
3 - Расположите в порядке возрастания числа(все числа даны в градусах): sin...
1 - Вбарометре-анероиде нарушилась герметизация металлической коробочке и в...
1
Давайте рассмотрим треугольник ABC. Так как F является точкой пересечения медиан AD и BE, мы можем сказать, что площадь треугольника ADF равна площади треугольника BDF. Пусть площадь каждого из этих треугольников равна x.
Теперь мы должны найти площадь треугольника DEF. TREDB площадь треугольника DEF состоит из суммы площадей треугольников DAF и DBF. Мы можем записать это как:
площадь DEF = площадь DAF + площадь DBF
Так как площадь треугольников DAF и DBF равны x (потому что медиана делит два треугольника на равные по площади части), то мы можем заменить эти значения в формуле:
площадь DEF = x + x
Теперь мы знаем, что площадь треугольника ABF равна 12. Мы можем записать это как:
площадь ABF = площадь ADF + площадь BDF
Заменим значения площадей треугольников ADF и BDF на x в формуле:
12 = x + x
Теперь нам нужно решить это уравнение, чтобы найти значение x. Мы можем объединить слагаемые x:
12 = 2x
Теперь разделим обе стороны уравнения на 2:
6 = x
Таким образом, мы нашли, что x (или площадь каждого из треугольников ADF и BDF) равно 6.
Теперь можем найти площадь треугольника DEF, используя формулу:
площадь DEF = площадь DAF + площадь DBF
= x + x
= 6 + 6
= 12
Таким образом, площадь треугольника DEF равна 12.