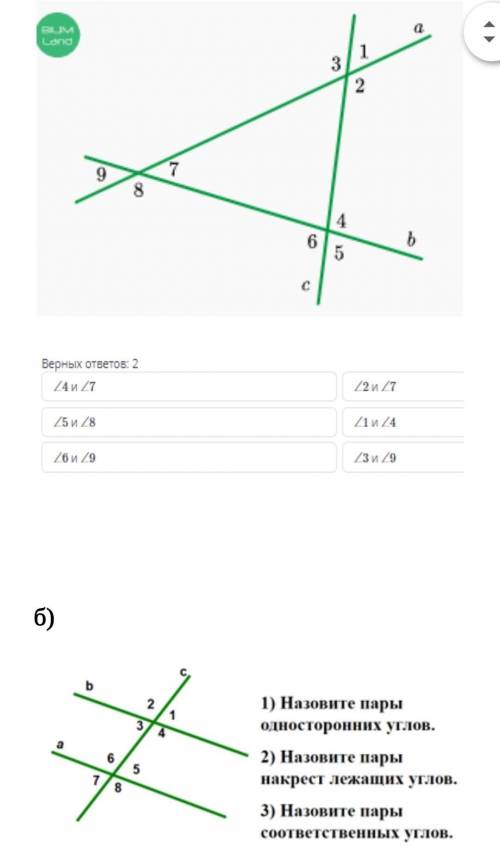
если прямая (а) является секущей, найди на рисунке соответственные углы ​

L3 и L9

Объяснение:

если онлайн мектеп то правелно

В данном случае, прямая (а) является секущей, то есть она пересекает две параллельные прямые. Найдем соответственные углы, то есть углы, которые находятся по одну и ту же сторону от секущей прямой и находятся на одинаковом расстоянии от основных параллельных прямых.

На рисунке дано, что прямая (b) параллельна основной параллельной прямой, и прямые (a) и (b) пересекаются в точке С.

Для нахождения соответственных углов, нам необходимо найти пары углов.

Первая пара углов образуется углами ACB и DCE. Они являются вертикальными углами, так как они находятся на пересекающихся прямых и находятся напротив друг друга. Вертикальные углы всегда равны друг другу.

Вторая пара углов образуется углами ECD и FCG. Они также являются вертикальными углами. Поэтому углы ECD и FCG также равны.

Третья пара углов образуется углами FCG и HCG. Они являются соответствующими углами, так как находятся на разных линиях и находятся на одинаковом расстоянии от основных параллельных прямых. Поэтому углы FCG и HCG также равны.

Итак, соответственные углы на рисунке:
∠ACB = ∠DCE
∠ECD = ∠FCG
∠FCG = ∠HCG

Эти углы равны и могут быть выражены числами в градусах или с использованием специальных геометрических обозначений для углов (например, ∠ACB = 90° или ∠ACB = ∠DCE).

Таким образом, соответственные углы на данном рисунке равны друг другу и можно использовать это свойство для решения задач, связанных с пересечением секущей прямой и параллельных прямых.