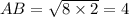Двокружности радиусов 2 и 8 касаются друг друга внешним образом в точке а общая касательная к ним проведена через точку а пересекает другую общую касательную в точке b найдите ab
Другие вопросы по теме Геометрия
Популярные вопросы
- 676. Выполните действия:1) 85,6 : (20,2 – 18,51) + 13,136; по...
1 - Послушайте отрывок из 18-и главы Гибель Атлантиды .какой стала...
1 - Что случилось с путниками в дороге? Кого они встретили Тема Александр...
3 - В равнобедренном прямоугольном треугольнике ABC с площадью 48...
3 - Векторы AC = a и BD =b служат диагоналями параллелограмма ABCD....
1 - Какие устойчивые степени окисления у сероводорода?...
2 - Вставь пропущенные окончания вопроса и имени прилагательного....
2 - Сколько аммиака можно получить из 89,6 л водорода при выходе...
1 - Вставь пропущенные окончания Вопроса и имениприлагательного.?)...
2 - Что может вызвать выподения волос? Впрос по биологии за отв...
2
Пусть O'A = R, OA = r; По свойству касательных из одной точки: BT = BA = BK; Значит BO и BO' - биссектрисы углов TBA и ABK; Отсюда угол OBO' прямой. BA перпендикулярен OO'. По свойству высоты, проведенной из вершины прямого угла: ; R = 8, r = 2, получаем:
; R = 8, r = 2, получаем: