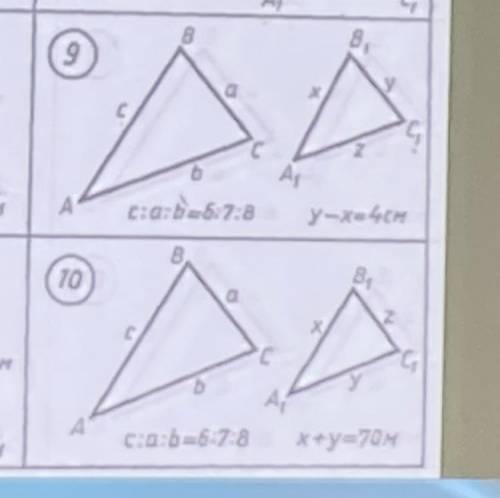
Две задачи практически одинаковые на тему признаки и подобие треугольников. не понимаю, как можно найти одну из сторон второго треугольника, если известно y-x=4 найти нужно x,y,z
по условию два треугольника подобны (abc~a1b1c1)

подскажите

Окей, давай разберем эту задачу по шагам.

Задача говорит нам, что два треугольника подобны. Подобные треугольники имеют соответствующие стороны, пропорциональные.

Мы знаем, что одна из сторон второго треугольника равна y-x=4. Для того чтобы найти остальные стороны второго треугольника, нам нужно знать соотношение между сторонами двух треугольников.

Известно, что треугольники подобны, поэтому любая сторона первого треугольника будет пропорциональна соответствующей стороне второго треугольника.

Начнем с пропорций между сторонами двух треугольников. Обозначим стороны первого треугольника как a, b и c, а стороны второго треугольника как a1, b1 и c1.

Мы можем записать следующие пропорции:
a/a1 = b/b1 = c/c1

Теперь у нас есть две этих пропорции:
a/a1 = b/b1 (Уравнение 1)
a/a1 = c/c1 (Уравнение 2)

Затем нам нужно использовать информацию, что y-x=4, чтобы связать это с пропорциями.

Используя уравнение 1, мы можем сказать, что a = (b * a1)/b1.

Теперь мы можем заменить a в уравнении 2 с использованием этого равенства:
(b * a1)/b1 / a1 = c/c1

Мы можем упростить это выражение:
b / b1 = c / c1

Теперь у нас есть уравнение, которое связывает все стороны треугольников.

Мы также знаем, что известная нам сторона второго треугольника равна y-x=4. Предположим, что эта сторона - b1.

Теперь, используя пропорцию b / b1 = c / c1, мы можем записать:
b / 4 = c / c1

Теперь у нас есть два неизвестных: b и c1. Но мы можем использовать другую информацию в задаче, чтобы решить эту систему уравнений.

Нам также известно, что b + c = z. Мы можем записать это в уравнении:
y - x + c1 = z

Мы также знаем, что y - x = 4, поэтому мы можем записать:
4 + c1 = z

Теперь у нас есть два уравнения, которые связывают b и c1, и z. Мы можем решить эту систему уравнений, чтобы найти значения b, c1 и z.

Одно из возможных решений заключается в том, чтобы предположить, что b = 2 и c1 = 3. Тогда мы можем использовать эти значения, чтобы найти z:
4 + 3 = z
z = 7

Таким образом, если b = 2, c1 = 3 и z = 7, мы можем решить эту задачу.

Но нужно помнить, что это всего лишь одно из возможных решений. Может быть и другие значения b, c1 и z, которые соответствуют условиям задачи.

Надеюсь, что это решение помогло тебе понять, как найти одну из сторон второго треугольника, если известно y-x=4. Если у тебя есть еще вопросы или что-то непонятно, не стесняйся обратиться ко мне.