Дві сторони трикутника дорівнюють 12 і 18 см, а бісектриса кута між ними ділить третю сторону на відрізки, різниця між якими дорівнює 4 см. Знайдіть периметр трикутника.

Ответы

Швабу 11.10.2020 05:15

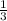ответ: 35 $\frac{1}{3}$ см

Объяснение:

Намалюй трикутник АВС

АВ = 12 см, АС = 18 см

З вершини кута А проведена бісектриса АМ, яка ділить сторону ВС на відрізки ВМ і МС.

1) Нехай відрізок ВМ буде х см, тоді відрізок МС буде х + 4 см (за умовою).

2) 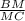$\frac{AB}{AC}$ = $\frac{BM}{MC}$ - за теоремою бісектриси.

$\frac{12}{18}$ = $\frac{x}{x+4}$

12(x+4) = 18x

12x + 4 = 18x

6x = 4

x = $\frac{4}{6}$ = $\frac{2}{3}$ см

Значить відрізок ВМ дорівнює $\frac{2}{3}$ см, а відрізок МС 4 $\frac{2}{3}$ см.

Сторона ВС = ВМ + МС

ВС = 5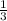 $\frac{1}{3}$ см

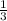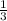2) Р ΔАВС = 12 + 18 + 5 $\frac{1}{3}$ = 35 $\frac{1}{3}$ см.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

Oven463 15.06.2019 04:00

veronika1217 15.06.2019 04:00

sokolovsokol3андрей 15.06.2019 04:00

VolhaRednaya8 18.03.2019 18:40

Уравнение прямой 12x-5y-65=0 к виду y=kx+b...

ольга2224 20.12.2019 11:17

BackTiger007 20.12.2019 11:15

platymax 20.12.2019 11:15

gbn2r56 20.12.2019 11:14

Найдите искомые отрезки по данным рисунка 3...

yulia24082 20.12.2019 11:11

Вичка03 20.12.2019 11:09