Доведіть,що рівняння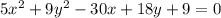
визначає еліпс. Знайти координати його центру С, півосі, ексцентриситет, рівняння директрис.​

Виділяємо повні квадрати:

для x: 5 (x²-2 * 3x + 3²) -5 * 3² = 5 (x-3) ²-45,

для y: 9 (y² + 2 * 1y + 1) -9 * 1 = 9 (y + 1) ²-9.

В результаті отримуємо: 5 (x-3) ² + 9 (y + 1) ² = 45

Розділимо всі вираз на 45: ((x-3) ² / 9) + ((y + 1) ² / 5) = 1.

Параметри кривої - це еліпс, його півосі a = 3 і b = √5.

Центр еліпса в точці: C (3; -1)

Координати фокусів F1 (-c; 0) і F2 (c; 0), де c - половина відстані між фокусами: F1 (-2; 0), F2 (2; 0). з = √ (9 - 5) = + -√4 = + -2.

З урахуванням центру, координати фокусів рівні:

F1 ((- 2 + 3) = 1; -1), F2 ((2 + 3) = 5; -1).

Ексцентриситет дорівнює: е = с / а = 2/3.

Внаслідок нерівності c <a ексцентриситет еліпса менше 1.

кхм кхм я хз) так что сори братан