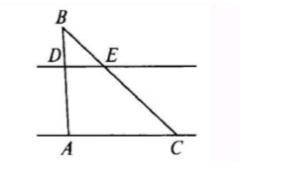
Докажите подобие и и решите задачу. Дано: DE||АС; BD = 3,1 см, BE = 4,2 см, ВА = 9,3 см, ВС = 12,6 см (рис. № 1).
Найти, a) DE : АС, б) PАВС : PDBE, в) SDBE : SABC.

Докажем подобие треугольников:

1) угол B - общий

2) угол BDE = углу BAC (т.к. прямые)

Значит, треугольник подобны по двум углам.

Прямые параллельны, т.к. сумма односторонних углов = 180.

DE/AC=BE/BC = 4.2/12.6=1/3

P1/P2 = BA/BD=9.3/3.1=3/1

S2/S1=(BE/BC)^2=1/9

Объяснение:

если что ^2 означает что нужно писать с верху цифру

Для начала, давайте разберемся с понятием подобия треугольников. Два треугольника считаются подобными, если их соответствующие углы равны, и их соответствующие стороны пропорциональны.

В данной задаче, мы имеем треугольники ABC и DBE. Дано, что DE параллельна AC. Из этого следует, что угол D и угол B являются соответственными углами, так как они находятся между параллельными прямыми AC и DE. То есть, угол D = угол B.

Теперь, чтобы доказать подобие треугольников, нам нужно убедиться, что их стороны пропорциональны.

Для начала, рассмотрим отношение сторон DE и AC. Мы имеем DE = 4,2 см и AC = 9,3 см. Теперь смотрим на соответствующую сторону в треугольнике DBE, которая является стороной DB. У нас имеется DB = 3,1 см.

Для доказательства подобия, мы должны убедиться, что отношение сторон DE и AC равно отношению сторон DB и BC.

Таким образом, DB/BC = DE/AC.

Подставляя известные значения, получаем: 3,1/BC = 4,2/9,3.

Мы можем упростить это уравнение, умножив обе стороны на 9,3: 3,1/BC * 9,3 = 4,2.

Теперь делим 3,1 на 4,2, чтобы найти значение BC: BC ≈ 3,022.

Таким образом, мы доказали подобие треугольников ABC и DBE, поскольку их стороны пропорциональны.

Теперь перейдем к решению задачи:

а) DE : AC:
Мы уже выяснили, что DE/AC = DB/BC. Подставим значения: DE/AC = 4,2/9,3. Делим 4,2 на 9,3, чтобы получить значение DE/AC: DE/AC ≈ 0,452.

б) PABC : PDBE:
Периметр треугольника ABC обозначим как PABC, а периметр треугольника DBE обозначим как PDBE.
PABC = AB + BC + AC = 9,3 + 3,022 + 12,6 = 24,922.
PDBE = DB + BE + DE = 3,1 + 4,2 + 4,2 = 11,5.

Теперь найдем отношение периметров: PABC/PDBE = 24,922/11,5 ≈ 2,165.

в) SDBE : SABC:
Площадь треугольника ABC обозначим как SABC, а площадь треугольника DBE обозначим как SDBE.
Для нахождения площади треугольника ABC, мы можем использовать формулу для площади треугольника, основанную на длинах его сторон и синусе угла между ними: S = 0,5 * AB * BC * sin(∠B).
SABC = 0,5 * 9,3 * 3,022 * sin(∠B) ≈ [(0,5 * 9,3 * 3,022)/BC] * sin(∠B). Здесь мы использовали отношение сторон DE/AC = DB/BC.
SDBE = 0,5 * 3,1 * 4,2 * sin(∠B) = [(0,5 * 3,1 * 4,2)/BC] * sin(∠B).

Теперь найдем отношение площадей: SDBE/SABC ≈ [(0,5 * 3,1 * 4,2)/BC] * sin(∠B) / [(0,5 * 9,3 * 3,022)/BC] * sin(∠B).
Заметим, что BC упрощается.
SDBE/SABC ≈ (3,1 * 4,2)/(9,3 * 3,022) ≈ 0,514.

Таким образом, мы получили ответы на все три подзадачи:
а) DE : AC ≈ 0,452.
б) PABC : PDBE ≈ 2,165.
в) SDBE : SABC ≈ 0,514.