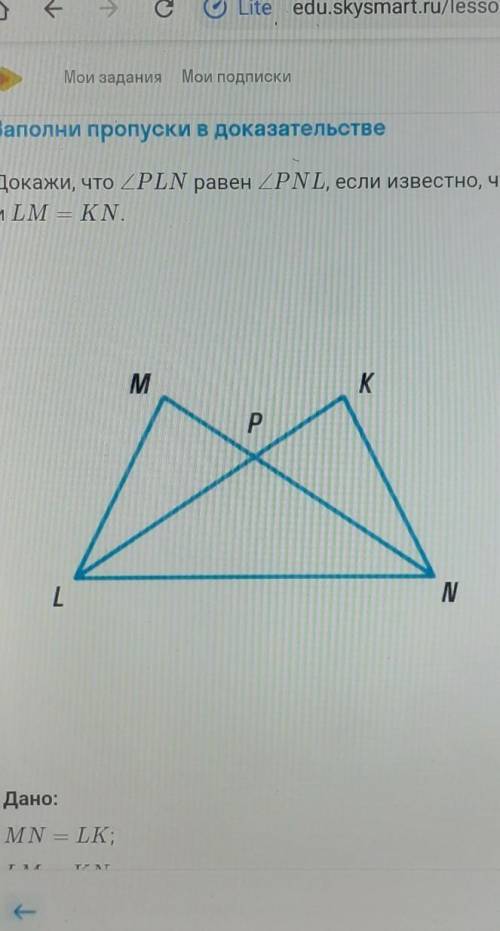
Докажите что угол PLN равен углу PNL,если известно, что MN=Lk и LM=KN.
Другие вопросы по теме Геометрия
Популярные вопросы
- Верны ли следующие суждения оверны ли следующие суждения о моральных ценностях?...
3 - Являются тропами: оксюморон, литота, антитеза, аллегория...
1 - Какие чуства мешают взаимопониманию людей? какие чества взаимопониманию людей?...
1 - Что экспортирует япония? в какие страны? страна - товар....
3 - Вравенстве 18*12*3*1=21 вместо* поставили знаки арифметических действий так,...
2 - Решить пример. m-8 : m(в степени 2) - 64 8m 15m(в степени 2)...
1 - Составить сочинение на тему один день среднивикового рыцаря .буду ....
2 - Исключите лишнее 1. na, h2o, si, ca 2. hcl, h2o, nh3, h2 3. scl2, cacl2, mgcl2,...
2 - Что такое закономерность чисел? 111 5 222 4...
3 - Верны ли следующие суждения о верны ли следующие суждения о моральных ценностях?...
2
Рассмотрим треуг. MLN и треуг. KLN:
1)MN=LK(по условию)
2)LM=KN(по условию)
3)LM-общая сторона
=> MLN=KLN(по третьему признаку равенства треугольников)
=> угол PLN= углу PNL
Нам нужно доказать, что угол PLN равен углу PNL.
Чтобы доказать это, нам понадобится использовать свойства равенства треугольников.
1. Рассмотрим треугольники MPL и NKL. У нас есть две равные стороны: LM = KN и MP = NK. Поэтому эти два треугольника равны по стороне-стороне-стороне (SSS).
2. SSS гарантирует, что углы MPL и NKL также равны. Это следует из теоремы о равных треугольниках, где соответствующие углы равны.
3. Теперь рассмотрим треугольники MPL и NLP. У нас есть две равные стороны: MP = NL и LM = LP.
4. Кроме того, мы знаем, что углы MPL и NKL равны (из пункта 2).
5. Опять же, используя SSS, мы можем сделать вывод, что треугольники MPL и NLP равны.
6. Это означает, что соответствующие углы у этих треугольников также равны.
Таким образом, угол PLN равен углу PNL.
Это завершает наше доказательство.