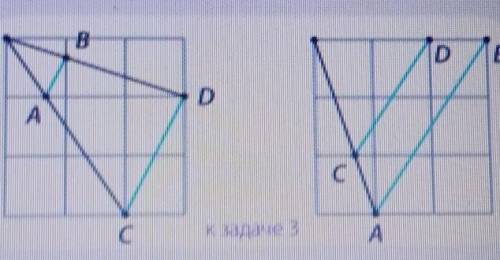
Докажите что прямые ав и сд на клетчатой бумаге параллельны
Другие вопросы по теме Геометрия
Популярные вопросы
- Решите уравнение: x/6 + 1 = (x – 1)/5...
1 - По действиям, подсказку ответ саша заработал 384, а миша 420д. рабочие...
3 - Напишите 10 примеров примыкания из капитанской дочки...
2 - Да воз и ныне там из какого произведения...
2 - Прочитай текст и ответь на заданные вопросы. разрешить спор. максим...
3 - Мальчик при расчёте с кассиром совсем запутался .если он купит 9 марок,то...
3 - Может ли польша войти в элиту стран?...
3 - Напишите сочинение про улица мира 20 по и еще перевод по русс...
2 - Read the text and fi ll in the blanks (1—6) with the parts of the sentences...
1 - Какой год был раньше : 40год до н. э. или 20год н. э. ? на сколько...
3
Определение параллельности прямых гласит: "Две прямые на плоскости называются параллельными, если они не пересекаются и ни в одной точке не лежат на одной прямой".
Давайте взглянем на клетчатую бумагу. Мы видим, что прямая ав и прямая сд проходят через параллельные отрезки линий с прямым углом и не пересекаются.
Мы также можем использовать понятие угловых линий. Угловая линия - это линия, которая пересекает две параллельные линии и создает угол с каждой из них. Если бы ав и сд были пересекающимися прямыми, то угловая линия пересекала бы каждую из них в разных точках, что нарушает геометрическую природу угловых линий. Однако у нас нет таких пересечений - угловая линия не пересекает параллельные прямые ав и сд и не создает углы с ними.
Таким образом, на основании определения параллельности и наблюдений о клетчатой бумаге, мы можем утверждать, что прямые ав и сд на клетчатой бумаге параллельны.