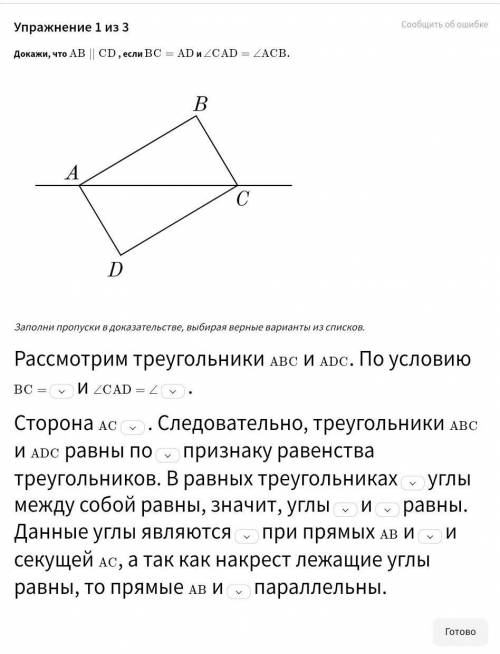
Докажи, что AB ∣∣ CD , если BC=AD и CAD=ACB
Другие вопросы по теме Геометрия
Популярные вопросы
- На окисление элемента массой 3,2 г потребовался кислород объёмом 0,56...
2 - Как доказать. что средняя линия трапеции проходит через середины диагоналей...
1 - .(Машина за 6 минут может вырыть канаву в 1 метр, какой длины канаву выроет...
3 - .(Решите систему уравнений, используя подстановки: x+y=4 y+xy=6)....
1 - .(Машина за 6 минут может вырыть канаву длиной в 1метр. какой длины канаву...
1 - .(Акак найти площадь треугольника, если его медианы равны 9см,12см,15см.)....
1 - .(Из раздела княжеская русь-украина вы узнали о многих князьях, живых...
1 - Еи f- середина сторон ав и вс треугольника авс. найдите еf и угол bef,...
3 - Три числа которые больше чем т 6,44 но меньше чем 6,46...
3 - Почему спартанцам запретили двадцать лет появлятся на олимпийских играх...
2
BC = AD и <CAD = <ACB
Сторона AC - общая, ABC и ADC равны по 1-му признаку равенства треугольников.
В равных треугольниках все углы равных, значит углы <BAC = <DCA. данные углы являются накрест лежащими при прямых AB и CD, то прямые AB и CD параллельны.
Надеюсь понятно написал
Шаг 1: Поскольку мы знаем, что CAD=ACB, мы можем использовать свойство углов равных биссектрис. Это значит, что мы можем сказать, что угол CAD и угол ACB равны.
Шаг 2: Теперь, когда у нас есть равные углы, мы можем использовать свойство углов равных оснований. Это значит, что мы можем сказать, что угол ABC равен углу ACD.
Шаг 3: Из шага 2 мы также знаем, что углы ABC и ACD равны. Это значит, что у граничных углов треугольника ABC есть равные значения.
Шаг 4: Поскольку у нас есть две пары равных граничных углов, мы можем использовать свойство параллельных линий, которое говорит, что если у двух треугольников с двумя парными равными граничными углами, то их третьи стороны параллельны.
Шаг 5: Это означает, что отрезки AB и CD параллельны.
Таким образом, на основе данных о равных углах и свойства параллельности мы доказали, что отрезки AB и CD параллельны.