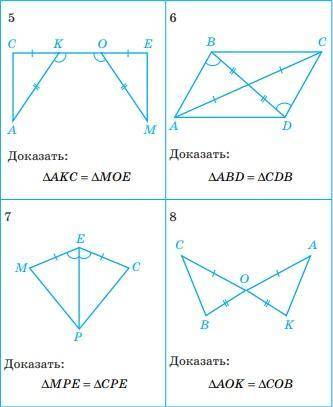
Доказать под номеров 5,6,7.

Для решения данной задачи, давайте рассмотрим каждую подзадачу по отдельности.

Подзадача №5:
На данном рисунке даны две прямые, AB и CD, которые пересекаются в точке O. Мы должны доказать, что угол AOC равен углу BOD.

Для начала, вспомним некоторые правила:
1) При пересечении прямых, образуются вертикальные углы, которые равны между собой.
2) Если угол равен вертикальному углу, то он равен каждому из углов, созданных пересекающимися прямыми.

Исходя из этих правил, мы можем утверждать, что угол AOC равен углу AOB (так как они вертикальные) и углу BOD, поскольку угол AOB и угол BOD - это один и тот же угол. Таким образом, угол AOC равен углу BOD.

Ответ: Мы доказали, что угол AOC равен углу BOD.

Подзадача №6:
Дано: AO и CO являются высотами треугольника ABC.

Мы должны доказать, что треугольник AOC равнобедренный (то есть, AO=CO).

Для решения данной задачи, воспользуемся свойствами высот треугольника:

1) Высота треугольника перпендикулярна соответствующей стороне.
2) Высоты треугольника пересекаются в одной точке, называемой ортоцентром.

Исходя из этих свойств, мы можем утверждать, что высоты AO и CO перпендикулярны стороне AC. Поскольку углы прямые, мы можем сделать вывод, что треугольник AOC - прямоугольный.

Также, поскольку ортоцентр треугольника является точкой пересечения всех высот, можно утверждать, что точка O, в которой пересекаются высоты AO и CO, равноудалена от сторон AB и BC.

Таким образом, треугольник AOC является прямоугольным и равнобедренным, что означает, что AO=CO.

Ответ: Мы доказали, что треугольник AOC является равнобедренным.

Подзадача №7:
Дано: BC является перпендикуляром к AO, и треугольник ABC является равнобедренным, при этом BC не является основанием треугольника.

Мы должны доказать, что угол OBC равен углу BOC.

Для решения данной задачи, используем свойства равнобедренных треугольников:

1) Равнобедренный треугольник имеет две равные стороны.
2) Биссектриса угла равнобедренного треугольника делит противоположную сторону на две равные части, а также образует равные углы с боковыми сторонами.

Исходя из этих свойств, мы можем утверждать, что AO равно CO. Поскольку BC перпендикулярна AO, мы можем сделать вывод, что угол OBC равен углу BOC.

Ответ: Мы доказали, что угол OBC равен углу BOC.