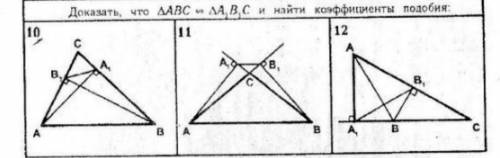
Доказать что треугольник АВС подобен треугольнику А1В1С1 и найти коэффициенты подобия

Для доказательства подобия треугольников АВС и А1В1С1, мы должны проверить выполнение двух условий подобия: соответствующие углы равны, а соответствующие стороны пропорциональны.

1. Проверка равенства углов:
В треугольниках АВС и А1В1С1 мы видим три пары соответствующих углов: ∠А = ∠А1, ∠В = ∠В1 и ∠С = ∠С1. Заметим, что углы этих пар соответственных углов являются вертикальными углами, которые равны между собой. Таким образом, углы треугольников АВС и А1В1С1 равны.

2. Проверка пропорциональности сторон:
Чтобы проверить пропорциональность сторон, необходимо сравнить длины сторон треугольников АВС и А1В1С1 и установить, есть ли между ними определенное отношение.

Для этого мы можем рассмотреть отношение длин одной из сторон в каждом треугольнике. Например, длины сторон АВ и А1В1.

Длина стороны АВ равна 4 см, а длина соответствующей стороны А1В1 равна 2 см.

Теперь найдем отношение длин сторон этих треугольников:
AB / A1B1 = 4см / 2см = 2

Мы получили, что отношение длины сторон АВ и А1В1 равно 2. Это значит, что стороны данных треугольников пропорциональны.

Таким образом, мы доказали, что треугольники АВС и А1В1С1 подобны.

Коэффициент подобия это отношение длин соответствующих сторон треугольников. В нашем случае, коэффициент подобия равен 2. Это означает, что каждая сторона треугольника АВС в 2 раза больше соответствующей стороны треугольника А1В1С1.