Доказать что при пересечении двух параллельных прямых секущей соответственные углы равны
Ответы
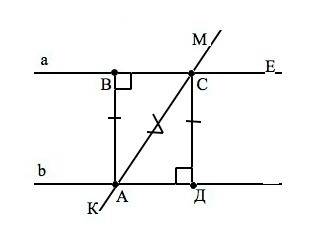
Пусть прямые а и b параллельны, МК – секущая, А и С - точки пересечения между параллельными прямыми и секущей (см. рисунок приложения) Расстояние между параллельными прямыми одинаково на всём их протяжении и равно длине отрезка, проведенного между ними перпендикулярно. АВ и СД – равные катеты получившихся прямоугольных треугольников АВС и АДС с общей гипотенузой АС. Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны. Из равенства ∆ АВС и ∆ АДС. следует равенство всех их сходственных элементов. ⇒ ∠ВСА=∠САД. Но ∠ВСА=∠ЕСМ как вертикальный, а угол ЕСМ - соответственный углу САД. ⇒ Соответственные углы при пересечении двух параллельных прямых третьей прямой – секущей – равны.
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Рассчитайте относительные молекулярные массы веществ, формулы которых: h2s, so3,...
1 - Найти проекцию точки а(3; -1) на прямую 4x+3y=6...
3 - найти причастия и деепричастия из . 47 ( язык)8 класс коровина 10...
1 - Написать сочинение по комедии фонвизина недоросль по плану : 1-проблема стоящая...
3 - Язык номер 75 б выпишите из предложения словосочетания существительных и прилагательных...
2 - Укажите область значений функции: [tex]1)y = {x}^{2} + 1 [/tex][tex]2)y = - \sqrt{x}...
3 - Написать правильно по казахскому языку на казахском языке с переводом , ...
3 - Какой из названных процессов или явлений, главным образом, обеспечивается видом...
2 - Лист за на відркиття музею...
3 - Решить информатика 7 класс электронная тетрадь ...
3