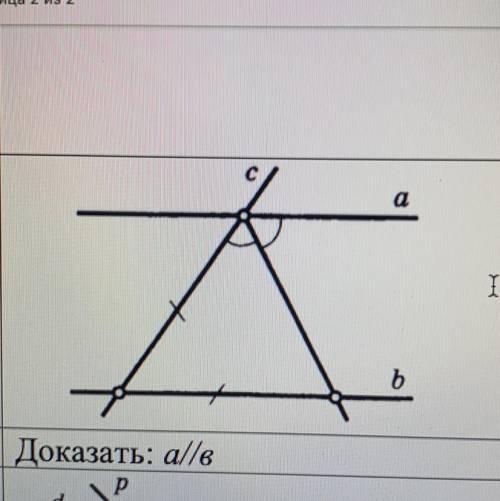
Доказать:a//b
(Все обозначения смотреть на рисунке)
Другие вопросы по теме Геометрия
Популярные вопросы
- На числовом луче с единичным отрезком 5 клеток отметь 1 целых дам за ответ...
1 - 2-тапсырма. Берлген сөз тіркестерін орыс тіліне аударып жаз. Атақты спортшы...
3 - 2 Complete the key phrases. Then look at the model text and check your answers.KEY...
1 - Классифицируйте по типам химических связей в данных соединениях: NaF, K2O,...
3 - Расположи в правильной последовательности этапы возникновения жизни на Земле...
1 - Составьте формулы кислых ортофосфатов Кальция, основных хлоридов Хрома (III)...
1 - РЕШИТЕ КАРТОЧКУ ПО РУССКОМУ ЯЗЫКУ ПРЕДЛОГИФОТКА ПРИКРЕПЛЕНА >...
3 - Гральну кістку кидають 80 разів. Знайдіть із ймовірністю 0,9973 межі, у яких...
2 - . Complete with the correct form Future Simple (will), to be going to, present...
2 - Запишите предложения и выполните задания. Верстах в пят..надцати нашёл я (ниже)...
2
По условию задачи, у нас есть два пересекающихся прямоугольника ABCD и PQRD.
Пересекающиеся прямые AC и PR являются проекциями боковой стороны PARQ на основание AD, следовательно, они параллельны (свойство 1).
Также, пересекающиеся прямые BD и PQ являются проекциями противоположной боковой стороны DBCP на основание AD, следовательно, они также параллельны (свойство 1).
Из свойств параллельных прямых (свойство 2) следует, что любые две пересекающиеся прямые, параллельные одной и той же третьей прямой, также параллельны между собой.
Таким образом, мы можем сказать, что AC || PR и BD || PQ.
Теперь рассмотрим треугольники PAR и PBD.
У нас есть следующие факты:
- прямые AC и PR параллельны (свойство 1)
- прямые BD и PQ параллельны (свойство 1)
- угол PAR и угол PBD являются соответственными вертикальными углами и, следовательно, они равны между собой (свойство вертикальных углов)
- угол PRA и угол PBD являются соответственными вертикальными углами и, следовательно, они равны между собой (свойство вертикальных углов)
Таким образом, треугольники PAR и PBD являются подобными по двум углам - углу A и углу P.
Из теоремы о параллельных прямых и подобных треугольников (теорема 1) следует, что если два треугольника подобны, то соответствующие стороны этих треугольников пропорциональны.
Поэтому, AB/DP = AR/BD.
Теперь перепишем полученное уравнение: AB/BD = AR/DP
Также, мы знаем, что AB = a и BD = b (из условия задачи).
Подставляя данные значения в уравнение, получаем: a/b = AR/DP.
Таким образом, мы доказали, что a/b = AR/DP, что означает, что a параллельно b.