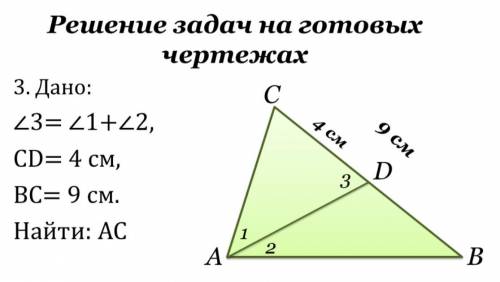
До меня только допёрло, что угол В равен углу 1.А дальше не идёт (ответ 6 см, но мне главное не сам ответ, а решение)

==========================================

Объяснение:

Т.к. сумма углов ∠1+∠2=∠3, а угол 3- внешний при вершине D в треугольнике  АВD, он равен сумме двух внутренних, не смежных с ним, то ∠В=∠1, угол С  в треугольнике АСD  равен

180°-∠1-(180-∠1-∠2)=180°-∠1-180+∠1-+∠2=∠2, тогда в треугольнике АВС сумма углов составляет ∠А+∠В+∠С=(∠1+∠2)+∠1+∠2=180°; или

2*(∠1+∠2)=180°, но тогда (∠1+∠2)=90°, а ∠3=90°, воспользуемся свойствами пропорциональных отрезков в прямоугольном треугольнике АСВ, в нем АD- высота, поэтому АС²=СD*СВ=9*4=36, тогда искомый катет АС=√36=6/см/

ответ 6см