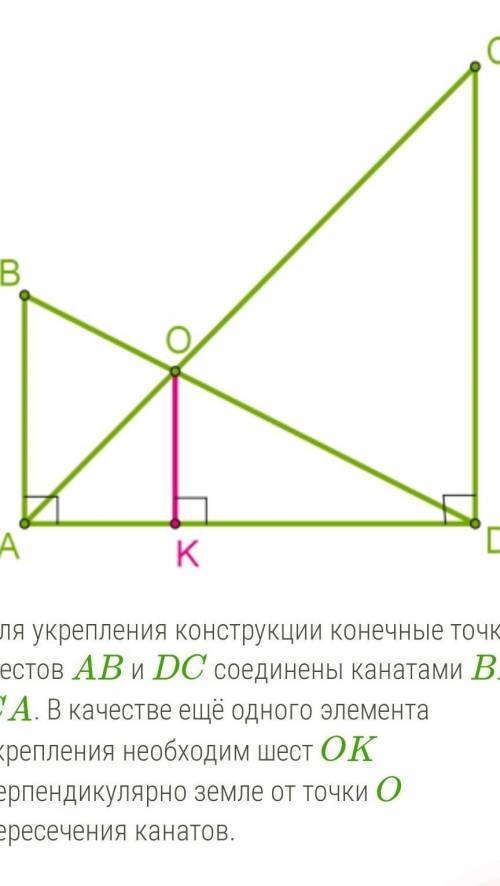
Для укрепления конструкции конечные точки шестов AB и DC соединены канатами BD и CA. В качестве ещё одного элемента укрепления необходим шест OK перпендикулярно земле от точки O пересечения канатов. 1. Докажи, что длина OK не зависит от расстояния AD между шестами, выразив длину OK через длины AB=x и DC=y.
2. Определи длину шеста OK, если AB= 4 м, а DC= 5 м.
1. Выражение через x и y (вначале записать нужно в окошке слагаемые с x, затем — с y, как в произведении, так и в сумме):
OK=
⋅
+
.
2. (Длину введи, округлив до сотых.)
OK=
м.
Другие вопросы по теме Геометрия
Популярные вопросы
- Представь дроби 1/5 1/4 в виде дробей со знаменателем...
1 - CuSO4+H2O2=H2SO4+CuO+O2 Как получить из полученного нами раствора серную...
1 - Какие преимущества получают кораллы, вступающие в симбиоз с динофитовыми...
2 - При переході з одного серидовища...
3 - Якщо вистрілити з дрібнокалібірної рушниці у варення яйце, то в яйце...
3 - Произведи морфологический разбор местоимения...
1 - ДРУЗЬЯ РЕШИТЬ КТО НИБУДЬ ПОСЛЕДНИЙ ПРИМЕР ОСТАЛЬСЯ Я СОВСЕМ НЕ ПОНИМАЮ...
2 - А)назовите органы выделения у растений. б) опишите структуру обозначеные...
2 - Эвропейский вибор Украины (Власне висловлення)Наведiть два докази (та...
2 - ИЛИ СКОЛЬКО ТУТ МОЖНО ДАТЬ ...
3
1. Докажем, что длина OK не зависит от расстояния AD между шестами, выразив длину OK через длины AB=x и DC=y.
Для начала, заметим, что треугольники AOB и COD являются прямоугольными, так как AO и DO - перпендикулярные высоты. Поэтому мы можем воспользоваться теоремой Пифагора для этих треугольников.
В треугольнике AOB:
AB^2 = AO^2 + OB^2
AB^2 = x^2 + OK^2 (1)
В треугольнике COD:
DC^2 = DO^2 + OC^2
DC^2 = y^2 + OK^2 (2)
Теперь мы можем сложить уравнения (1) и (2):
AB^2 + DC^2 = x^2 + OK^2 + y^2 + OK^2
AB^2 + DC^2 = x^2 + y^2 + 2OK^2
2OK^2 = AB^2 + DC^2 - x^2 - y^2
OK^2 = (AB^2 + DC^2 - x^2 - y^2)/2
OK^2 = (x^2 + y^2 - x^2 - y^2)/2
OK^2 = 0/2
OK^2 = 0
Из этого выражения следует, что OK^2 равно нулю, тогда и только тогда, когда AB^2 + DC^2 - x^2 - y^2 также равно нулю. Следовательно, длина OK не зависит от расстояния AD между шестами и выражается просто как OK = 0.
2. Определим длину шеста OK, если AB=4 м и DC=5 м.
Воспользуемся выражением OK^2 = (AB^2 + DC^2 - x^2 - y^2)/2:
OK^2 = (4^2 + 5^2 - 4^2 - 5^2)/2
OK^2 = (16 + 25 - 16 - 25)/2
OK^2 = 0/2
OK^2 = 0
Таким образом, длина шеста OK равна 0 метров.