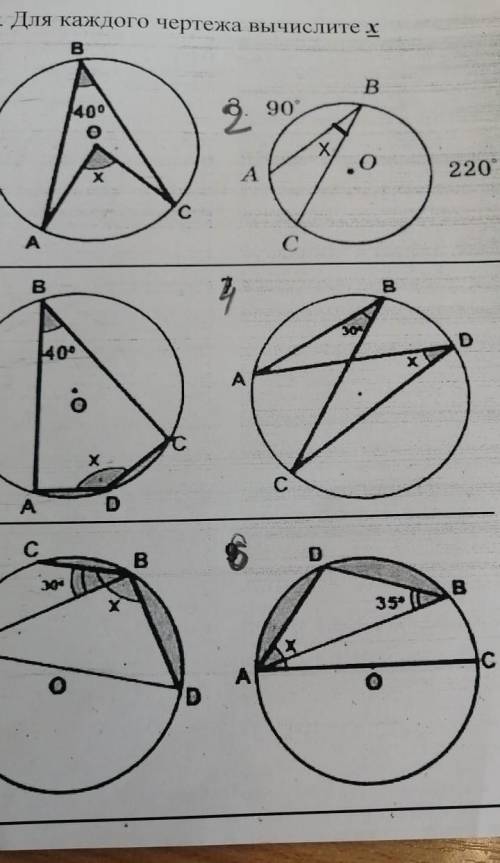
Для каждого чертежа вычислите х

Чтобы вычислить значение x для каждого чертежа, мы должны использовать правила и свойства алгебры и математических операций. Давайте посмотрим на каждый чертеж по очереди.

1. Чертеж с одной десятичной дробью:
На чертеже дана десятичная дробь вида 0,5x = 3. Чтобы найти значение x, мы должны переписать это уравнение, избавившись от десятичной дроби. Для этого умножим обе стороны уравнения на 10 (количество цифр после запятой в десятичной дроби). Получим:

10 * 0,5x = 10 * 3
5x = 30

Теперь нам необходимо избавиться от коэффициента перед x (в данном случае это число 5). Для этого мы поделим обе стороны уравнения на 5:

5x/5 = 30/5
x = 6

Таким образом, значение x для данного чертежа равно 6.

2. Чертеж с двумя десятичными дробями:
На чертеже дано уравнение 0,2x + 0,4 = 1,2. Чтобы найти значение x, мы должны избавиться от десятичных дробей, а затем найти значение x. Начнем с перевода десятичных дробей в обычные дроби. Заменим 0,2 и 0,4 на их эквиваленты в виде обычных дробей:

2/10x + 4/10 = 12/10

Теперь нам нужно привести коэффициенты перед x к общему знаменателю (в данном случае это число 10). Сложим дроби:

(2x + 4)/10 = 12/10

У нас теперь есть дробь с общим знаменателем. Если две дроби равны, то их числители также равны. Поэтому:

2x + 4 = 12

Теперь мы можем решить уравнение, избавившись от константы. Вычтем 4 с обеих сторон уравнения:

2x + 4 - 4 = 12 - 4
2x = 8

И наконец, разделим обе стороны уравнения на 2:

2x / 2 = 8 / 2
x = 4

Значение x для данного чертежа равно 4.

3. Чертеж с уравнением с дробью:
На чертеже дано уравнение (3/4)x = 9. Чтобы найти значение x, мы должны избавиться от дроби, а затем решить уравнение.

Чтобы избавиться от дроби, умножим обе стороны уравнения на обратную дробь (4/3):

(3/4)x * (4/3) = 9 * (4/3)

Сократим дроби:

(3 * 4 / 4 * 3)x = (9 * 4) / 3
1x = 36 / 3
x = 12

Значение x для данного чертежа равно 12.

Таким образом, мы рассмотрели каждый чертеж и вычислили значение x для каждого из них с помощью правил и свойств алгебры.