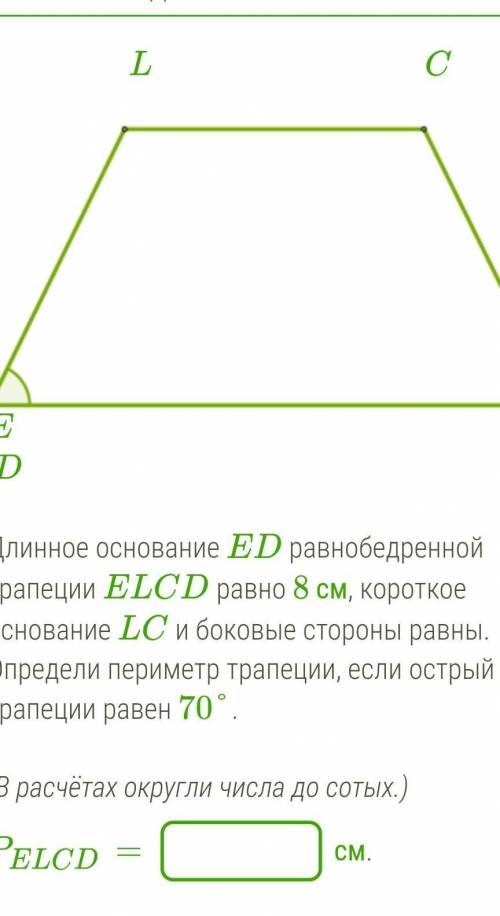
Длинное основание ED равнобедренной трапеции ELCD равно 8 см, короткое основание LC и боковые стороны равны. Определи периметр трапеции, если острый угол трапеции равен 70°. (В расчётах округли числа до сотых.)
PELCD=
см..​

Для решения этой задачи нам понадобится знание о свойствах равнобедренной трапеции и тригонометрии.

Дано, что длина длинного основания ED равна 8 см, короткое основание LC и боковые стороны равны.

Для начала, давайте обратим внимание на свойство равнобедренной трапеции, которое гласит, что углы при основаниях равны. Таким образом, у нас имеется две равные по величине длины стороны LC, и это значит, что угол ELC (острый угол) также является углом при основании и равен 70°.

Поскольку сумма углов в треугольнике равна 180°, мы можем вычислить величину угла LCE, равное 180° - 70° - 70° = 40°.

Следующим шагом мы можем обратиться к теореме синусов, чтобы найти длину боковой стороны LE. Теорема синусов гласит, что отношение длины стороны к синусу противолежащего ей угла одинаково для всех сторон и углов в треугольнике.

Согласно теореме синусов, мы можем записать:

sin(70°) / LE = sin(40°) / 8

Давайте найдем значение LE, перенеся и решив уравнение:

LE = (8 * sin(70°)) / sin(40°) ≈ 9.74 см (округляя до сотых)

Теперь у нас есть все три стороны LELC, и мы можем вычислить периметр PELCD равнобедренной трапеции:

PELCD = LC + LE + LD + EC
= 8 см + 9.74 см + 8 см + 8 см
≈ 33.74 см (округляя до сотых)

Таким образом, периметр PELCD равнобедренной трапеции составляет около 33.74 см.