1. Геометрия
  2. Диагонали ромба относятся как

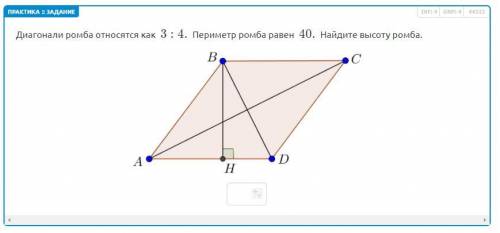
Диагонали ромба относятся как 3:4. Периметр ромба равен 40.
Найдите высоту ромба.


Диагонали ромба относятся как 3:4. Периметр ромба равен 40. Найдите высоту ромба.

Алeна1 Алeна1    2   29.12.2021 16:06    9

Ответы
anna47983 anna47983  29.12.2021 16:10

Пусть диагонали ромба пересекаются в точке О: АС ∩ ВD = О, диагонали ромба относятся как 3:4 ⇒ половины диагоналей ромба также относятся как 3:4 ⇒ можно обозначить: АО = 4х, ОВ = 3х. Периметр ромба равен 40 ⇒ его сторона равна 40 : 4 = 10,

АВ = ВС = СD = DА = 10. По теореме Пифагора:

АВ² = АО² + ВО² =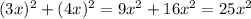 {(3x)^{2} + (4x)^{2} } = {9x^{2} + 16x^{2} } = {25x^{2} } = 10² = 100 ⇒

x² = 100 : 25 = 4 ⇒ x = 2 ⇒ АО = 4х = 4*2 = 8, ОВ = 3х = 3*2 = 6,

AC = 2AO = 2*8 = 16, ВD = 2ОВ = 2*6 = 12. Площадь ромба равна:

S = 0,5 * AC * ВD = BH * AD ⇒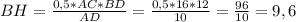 BH = \frac{0,5*AC*BD}{AD} = \frac{0,5*16*12}{10} = \frac{96}{10} = 9,6

ответ: высота ромба ВН равна 9,6


Диагонали ромба относятся как 3:4. Периметр ромба равен 40. Найдите высоту ромба.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
rubaqlo rubaqlo  30.11.2020 12:04
Два примера от защиты от атмосферных явления даю 50б​...
1dianalady1 1dianalady1  10.03.2019 07:20
Найти углы треугольника, если они образуют арифметическую прогрессию и наибольшая сторона треугольника в 2 раза больше за наименьшую...
arinakurbatovu arinakurbatovu  10.03.2019 07:20
Существует ли прямоугольный треугольник, у которого точка пересечения медиан лежит на кругу, который вписан в этот треугольник...
Bessihatanuamailru Bessihatanuamailru  10.03.2019 07:20
Найти радиус окружности вписанной в треугольник со сторонами 3,4 и 5...
Martinii1 Martinii1  10.03.2019 07:20
Две стороны треугольника равны 10 и 5, высота, проведенная к наименьшей равна 8, найти высоту проведенную у наибольшей...
ксения1279мпсалч ксения1279мпсалч  10.03.2019 07:20
Около окружности описана равнобокая трапеция авсd. угол между основаниями аd и боковой стороной ав равен 60 градусов. найти боковую сторону и основания трапеции, если радиус...
SVINKAPIPA SVINKAPIPA  10.03.2019 07:20
Вправильной треугольной пирамиде sabc m-середина ребра ab, s-вершина. известно, что bc=3, а площадь боковой поверхности пирамиды=45. найдите длину отрезка sm....
dim10102806 dim10102806  10.03.2019 07:20
Нужно! точка касания круга, вписанного в прямоугольный треугольник, дклит гипотенузу на части, равные 4см и 6 см. найдите площадь этого круга....
AliKsandraSm AliKsandraSm  10.03.2019 07:20
Три последовательные стороны описанной около круга трапеции равны 13 см, 8 см и 13см. найдите радиус круга....
daaanila2015 daaanila2015  10.03.2019 07:20
Площадь основания конуса равна 4п. если его высота в 1,5 раза больше радиуса, то площадь бок.пов.конуса.=...

Популярные вопросы