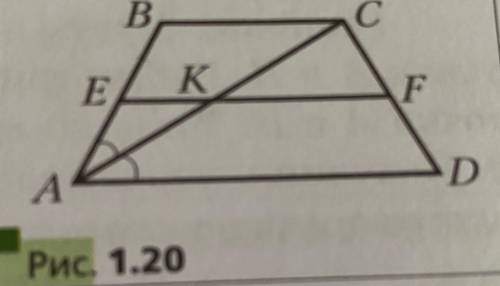
Диагональ AC равнобокой трапеции АВСD делит угол BAD пополам (смотрите рисунок). Точка E - середина отрезка AB. Прямая, проходящая через точку E параллельно основаниям трапеции, пересекает отрезок AC в точке К, а отрезок CD - в точке F. Найдите периметр трапеции ABCD, если EK = 3 см, KF= 5 см

Объяснение:

диагональ АС делит трапецию на 2 треугольника: АВС и АСД. Рассмотрим полученный ∆АСД. Так как точка Е - середина отрезка АВ, то точка F будет середина отрезка СД, следовательно EF является средней линией трапеции. Тогда KF будет являться средней линией ∆АСД (по теореме Фалеса: если прямая отсекает равные отрезки на одной стороне угла, то она отсекает равные отрезки и с другой стороны этого угла). По правилу треугольника его средняя линия=½ его основания, поэтому КF=½АД, или АД=2KF=5×2=10см

Если ЕF средняя линия трапеции, то она составит:

EK+KF=3+5=8см. Средняя линия трапеции вычисляется по формуле:

(ВС+АД)/2=EF. Используя эту формулу найдём сторону ВС:

перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:

ВС+10=8×2

ВС+10=16

ВС=16–10=6см

Рассмотрим ∆АВС. В нём <ВАС=<САД, поскольку диагональ АС биссектриса угла А. Так как ВС||АД, то <САД=<ВСА как внутренние разносторонние поэтому <ВАС=<ВСА, следовательно ∆АВС равнобедренный и АВ=ВС. Поскольку трапеция равнобедренная, то АВ=СД=ВС=6см

Теперь найдём периметр трапеции зная её стороны:

Р=АВ+ВС+СД+АД=6×3+10=18+10=28см

ОТВЕТ: Р=28 см