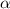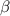Диагональ AC параллелограмма ABCD равна 5 и образует со сторонами углы и , один из которых тупой. Найдите площадь параллелограмма ABCD, если синус альфа = 12/13 и синус бета = 8/17 ответ округлите до сотых.

α-тупой угол, диагональ АС разбивает параллелограмм на два равных треугольника, в треугольнике АВС есть три угла α;β; (180-(α+β)); sin(180-(α+β))=sin(α+β)=sinα*cosβ+sinβ*cosα

cosβ=√(1-sin²β)=√(1-64/289)=√(225/289)=15/17;  

cosα=-√(1-sin²α)=-√(1-144/169)=-√(25/169)=-5/13;

sin(α+β)=(12/13)*(5/17)-(8/17)*(5/13)=(60-40)/(17*13)=20/(17*13);

По следствию из теоремы синусов АС/sin(180-(α+β))=BC/sinα=AB/sinβ;

5/(20/17*13)= BC/sinα;  BC=5*17*13*12/(13*20)=51

5/(20/17*13)=AB/sinβ; АВ=5*17*13*8/(17*20)=26

Значит, площадь равна АВ*АС*sin(α+β)=51*26*(20/17*13)=120

ответ 120,00

Посмотрел на задание, которое Вам предложили в качестве решения в комментариях. Проверил. ответ тот же. )