1. Геометрия
  2. Даны вершины треугольника

Даны вершины треугольника АВС: А (0;4), В (-2;4), С (-1;3). Найдите угол А в треугольнике АВС.

Лера9814 Лера9814    3   06.06.2020 18:22    1

Ответы
Anna19013 Anna19013  15.10.2020 13:18

Объяснение: два решения, так как не знаю какую тему проходите.

1. решение.

Найдем длины сторон.

АВ =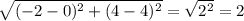\sqrt{(-2-0)^2+(4-4)^2} = \sqrt{2^2} = 2

AC =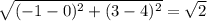 \sqrt{(-1-0)^2+(3-4)^2} = \sqrt{2}

BC =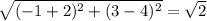 \sqrt{(-1+2)^2+(3-4)^2}=\sqrt{2}

По теореме косинусов

BC²=AB²+AC²-2AC*AB*cosA и отсюда

cosA =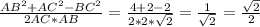 \frac{AB^2+AC^2-BC^2}{2AC*AB} = \frac{4+2-2}{2*2*\sqrt{2} } = \frac{1}{\sqrt{2}} = \frac{\sqrt{2} }{2}

Угол А = 45°

2 решение

Найдем координаты векторов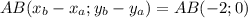 AB(x_b-x_a;y_b-y_a) = AB(-2;0)

Аналогично АС(-1;-1)

Найдем модули векторов

|AB| =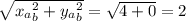 \sqrt{x_a_b^2+y_a_b^2} = \sqrt{4+0} = 2

Аналогично |AC| =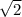 \sqrt{2}  кстати, модуль вектора и есть его длина и мы эти длины уже рассчитали выше.

Скалярным произведением двух векторов является сумма произведений соответствующих координат этих векторов.

(AB*AC) = (-2*(-1)) + 0*(-1)) = 2

Тогда из формулы скалярного произведения векторов АВ и АС

cosA =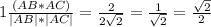 1\frac{(AB*AC)}{|AB|*|AC|} = \frac{2}{2\sqrt{2} } = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}

cosA = 45°


Даны вершины треугольника АВС: А (0;4), В (-2;4), С (-1;3). Найдите угол А в треугольнике АВС.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
missvolkova2001 missvolkova2001  03.06.2019 17:00
Докажите,что катет в прямоугольном треугольнике ,лежащий против угла в 30 градусов,равен половине гипотенузы. _ *...
premium79 premium79  02.02.2021 14:01
Изи сделайте просто болел я и тему не знаю 2вариант...
Saneitrix Saneitrix  02.02.2021 14:03
второй вариант 3 и 4 задание...
soldiertoy01 soldiertoy01  14.06.2019 05:00
Диагонали прямоугольника abcd пересекаются в точке о. найдите периметр треугольника aod, если ab - 9, bc - 12, bd - 15...
barmin2001g barmin2001g  01.04.2021 19:33
6. Через точку A (2; 3) проводят прямую, параллельную оси абсцисс. Найдите координаты его точки пересечения с осью ординат.​...
madamnowiczkai madamnowiczkai  01.04.2021 19:34
ОЧЕНЬ Знайти точки A (2; 0) - B (3; 2) при повороте на 90 ° по часовой стрелке...
кукла221 кукла221  30.07.2019 21:10
Высота прямоугольного параллелепипеда с квадратным основанием равна 60 см.диагональ параллелепипеда образует с плоскостью основания угол 60. градусов.найти объём параллелепипед...
95123451 95123451  30.07.2019 21:10
Параллельны ли прямые a и b ? на рисунке 1.-2.-3...
Ми55555 Ми55555  30.07.2019 21:20
Втреугольнике abc угол c равен 45°, ad- биссектриса угда. a, угол adb равен 70° найтм градусную меру угла b...
viktoriasvoya viktoriasvoya  30.07.2019 21:20
Вправильной четырёхугольной пирамиде длина стороны основания равна 14 см ,а боковое ребро 10 см. найдите полную поверхность и объём....

Популярные вопросы