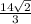Даны вершины треугольника а(3, –5), в(–3, 3), с(–1, –2). определить длину его биссектрисы, проведенной из вершины а.
Другие вопросы по теме Геометрия
Популярные вопросы
- Разбор слова применяется по составу, ....
1 - Каз.яз.надо вставить пропущенные слова. 1. өнер - қызыл тіл. 2. үй кісі бар,...
2 - Перевести на казахский: не больше 30% но не меньше 20%. на работе нужно для печати...
1 - Эрудит что такое фольклор допишите предложение фольклор это...
3 - Как изменяется род (если можно с примерами : ))...
2 - Из-за неблагоприятной погоды в этом году с молодой яблони собрали 5ящиков яблок...
2 - Решение и ответ номер 1 а) 7х+(9х++6х) б) 5-16х-9(4х-5) номер 2 24х+105=3+(13х-12)...
1 - Если у единорога убрать рог он будет лошадью или единорогом без...
1 - Запишите все трехзначные числа без повторения одинаковых цифр,используя цифры:...
2 - 2x+11=8x+10 решите с объяснением, не загадками, простыми словами, ....
3
Решение задания приложено
Найдем AB:
Аналогично AC=5, BC=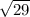
Найдем биссектрису:
ответ: