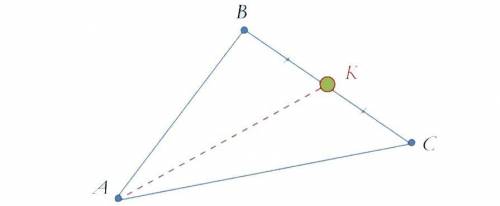
Даны вершины A(1;1), B(−1;5), C(5;5) треугольника ΔABC. Составить уравнение медианы AK, проведенной из вершины A ответ представить в видеy=k∗x+b
k=?
b=?
Другие вопросы по теме Геометрия
Популярные вопросы
- терміново, хто працює в python. 1. обчислити суму 10 довільних цілих...
2 - This is the time of the year many people suffer from high fever. *...
2 - запишите химические свойства спиртов на примере этанола. укажите сумму...
2 - ОЧЕНЬ НУЖНА ВАША Срок сдачи совсем скоро...
2 - Текст 1 Неряшливость в одежде – это, прежде всего, неуважение к окружающим...
1 - 1.Цепь состоит и з источника, амперметра, ключа и трех резисторов(...
2 - Найди расстояние между облаками если напряжение на облаках 200в а напряжение...
1 - Обчисліть будь ласка √54×96...
1 - Внутренний углы ∆ABC относятся как 2:3:7 найдите углы нужно ...
2 - 1/После тяжелой травмы появилась травма гортани и подвздошной кишки....
2
В данном случае, вершина A имеет координаты (1;1). Чтобы найти координаты точки K, необходимо найти среднюю точку отрезка BC, так как медиана делит отрезок BC пополам.
Получаем координаты средней точки:
xк = (xл + xk)/2,
yк = (yл + yк)/2.
В нашем случае, левая точка B имеет координаты (-1; 5), а правая точка C имеет координаты (5;5). Подставим их в формулу:
xк = (-1+5)/2 = 2,
yк = (5+5)/2 = 5.
Таким образом, координаты точки K равны (2;5).
Теперь, чтобы найти уравнение медианы AK, используем метод нахождения уравнения прямой по двум точкам.
Вначале найдем угловой коэффициент k.
k = (yк - ya) / (xк - xa),
где ya и xa - координаты точки A, yк и xк - координаты точки K.
Подставим значения и найдем k:
k = (5 - 1) / (2 - 1) = 4 / 1 = 4.
Теперь найдем свободный член b, подставив координаты точки A в уравнение прямой:
b = ya - k * xa = 1 - 4 * 1 = 1 - 4 = -3.
Таким образом, уравнение медианы AK, проведенной из вершины A, представляется в виде y = 4 * x - 3.
Итак, в ответе:
k = 4,
b = -3.