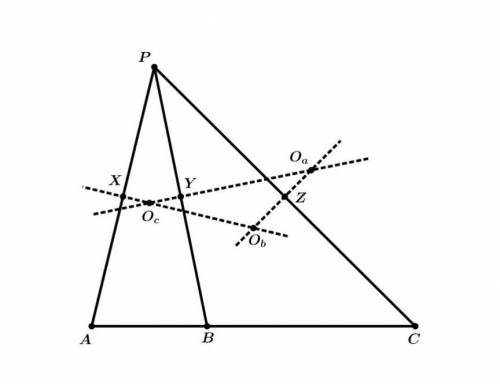
Даны точки A, B, C, лежащие на одной прямой, и точка P вне этой прямой. К отрезкам PA, PB, PC через их середины X, Y, Z проведём серединные перпендикуляры. Пусть они пересеклись в центрах Oa, Ob, Oc описанных окружностей треугольников PBC, PAC, PAB. Выберите на картинке 4 точки: 3 вершины треугольника и точку, лежащую на описанной окружности этого треугольника такие, что на картинке есть 3 точки, лежащие на прямой Симсона выбранной точки относительно выбранного треугольника. Все 7 точек должны быть различны.​

ObX, ObZ - серединные перпендикуляры

ObXP =ObZP =90 => XPZOb - описанный четырехугольник (POb - диаметр)

То есть Ob лежит на описанной окружности треугольника XPZ.

X, Z - основания перпендикуляров из Ob к сторонам треугольника XPZ.

Тогда XZ - прямая Симсона точки Ob относительно треугольника XPZ.

XY - средняя линия в APB, XY||AC

YZ - средняя линия в BPC, YZ||AC

Через точку Y можно провести только одну прямую, параллельную AC => точки X-Y-Z лежат на одной прямой.

Чтобы найти такие 4 точки, нам необходимо следовать следующим шагам:

Шаг 1: Построение серединных перпендикуляров
- Построим серединный перпендикуляр к отрезку PA через его середину X. Обозначим точку пересечения этого перпендикуляра с прямой BC как M.
- Построим серединный перпендикуляр к отрезку PB через его середину Y. Обозначим точку пересечения этого перпендикуляра с прямой AC как N.
- Построим серединный перпендикуляр к отрезку PC через его середину Z. Обозначим точку пересечения этого перпендикуляра с прямой AB как L.

Шаг 2: Построение центров описанных окружностей
- Поскольку Oa - центр описанной окружности треугольника PBC, то Oa будет лежать на перпендикуляре, проходящем через середину перпендикуляра, проведенного через точку M.
- Проведем перпендикуляр к прямой BC через точку M. Обозначим точку пересечения этого перпендикуляра с прямой AC как Oa.
- Аналогично, Ob и Oc будут центрами описанных окружностей треугольников PAC и PAB соответственно.

Шаг 3: Поиск точек на описанных окружностях
- Доберемся до изображения, чтобы найти 4 точки, удовлетворяющие условию.
- Выберем точки P, A, B, C согласно условию задачи.
- Для выбранного треугольника и центра его описанной окружности найдем точку на описанной окружности, которая лежит на прямой Симсона относительно этого треугольника. Эта точка будет четвертой точкой, удовлетворяющей условию задачи.