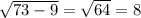Даны координаты вершин треугольника авс: а(-6; 1),d(2; 4),c(2; -2). докажите,что треугольник авс равнобедренный и найдите высоту треугольника,проведенную из вершины а.
Другие вопросы по теме Геометрия
Популярные вопросы
- Какой биотический фактор может ограничивать численность зелёного кузнечика?...
3 - А)из 225 кг руды можно получить 34,5кг меди. каково процентное содержание меди...
2 - Какое наибольшое трех значное число одновремено коратно 2 5 и 6...
1 - Сколько метров кружева потребуется даше, чтобы обшить 6 прямоугольников салфеток...
3 - Дочерти фигуру чтобы получился четырехугольник сторона равна 3 см...
3 - Противоположных направлениях отплыли теплоход и катер. скорость теплохода –...
2 - Первого дня на сто отремонтировали 38 автомашин.3 и 4 дня отремонтировали 36...
1 - Считая что π=3,14 определите длину окружности и площадь круга если радиус r=3,5...
1 - Выберите верные утверждения 1). если прямая пересекает одну из двух параллельных...
1 - Грузоподъёмность машины 3т. сколько учебников можно перевезти на такой машине...
1
В этом случае ищем длину AB, BC, AC.
Для этого пользуемся формулой: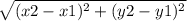
Отсюда АВ = корень из 64+9 = корень из 73;
ВС = 6, АС = корень из 73;
АВ и АС равны, поэтому АВС - равнобедренный.
Найдём выстоу АР. Для этого найдём ВР = ВС/2 = 3.
По т.Пифагора АР =