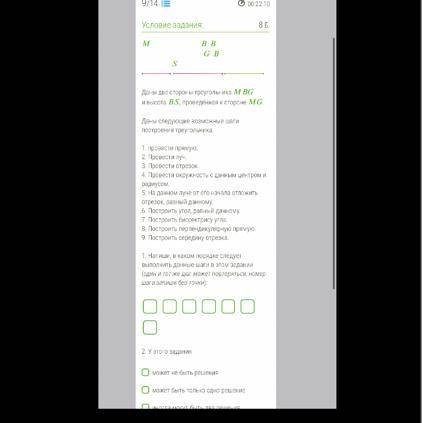
Даны две стороны треугольника MBG и высота BS, проведённая к стороне MG. Даны следующие возможные шаги построения треугольника:

1. провести прямую.
2. Провести луч.
3. Провести отрезок.
4. Провести окружность с данным центром и радиусом.
5. На данном луче от его начала отложить отрезок, равный данному.
6. Построить угол, равный данному.
7. Построить биссектрису угла.
8. Построить перпендикулярную прямую.
9. Построить середину отрезка.

1. Напиши, в каком порядке следует выполнить данные шаги в этом задании
(один и тот же шаг может повторяться, номер шага запиши без точки):

2. У этого задания

может не быть решения
может быть только одно решение
иногда могут быть два решения

Для того чтобы построить треугольник MBG и провести высоту BS, можно использовать следующие шаги:

1. Провести отрезок MG:
- берем циркуль и ложим его конец в точку M, если точка M еще не отмечена на листе, то проводим точку M;
- с другой стороны циркуля проводим отрезок через точку G так, чтобы он проходил через точку M и был достаточно длинным.

2. Построить перпендикуляр к отрезку MG через точку B:
- берем циркуль и ложим его конец в точку B;
- устанавливаем размер циркуля равным высоте BS;
- вращаем циркуль вокруг точки B и проводим дугу, которая пересекает отрезок MG в двух точках;
- проводим прямые линии через точки пересечения дуги и отрезка MG.

3. Обозначаем точку пересечения проведенного перпендикуляра с отрезком MG. Обозначим эту точку как S.

Теперь рассмотрим отдельно каждый из вопросов:

1. В каком порядке следует выполнить данные шаги в этом задании?
В данном задании не требуется заданным порядком выполнять шаги, так как можно выполнить шаги в любом порядке, и решение все равно будет верным.

2. У этого задания может не быть решения?
Нет, задание всегда имеет решение при условии, что две стороны треугольника MBG и высота BS действительны и можно построить.

3. Может быть только одно решение?
Да, в данном случае будет только одно решение, так как все данные точки и отрезки заданы однозначно.

Таким образом, можно построить треугольник MBG и провести высоту BS, используя описанные выше шаги, и в данном случае ответ на вопрос о количестве решений - одно решение.