Дано: треугольник авс а(1; 1),b(2,5),c(5,2) определить вид треугольника и еще вопрос нельзя не как аналетически это решить?

Найдем вектора, соответствующие сторонам этого треугольника:

AB = B-A = (1,4)

BC = C-B = (3,-3)

AC = C-A = (4,1)

Найдем длины векторов:

|AB| =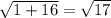  

|BC| =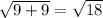   

|AC| =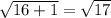    

Нетрудно видеть, что |AB| = |AC|

Следовательно треугольник равнобедренный.

Найдем скалярное произведение векторов и проверим, является ли треугольник прямоугольным:

AB*BC = (3-12) = -9

BC*AC = 12-3 = -9

AB*AC = 4+4 = 8

Скалярное произведение векторов ни в одном случае не равно нулю, следовательно треугольник не является прямоугольным.

ответ: Треугольник равнобедренный, равные стороны: AB = AC =