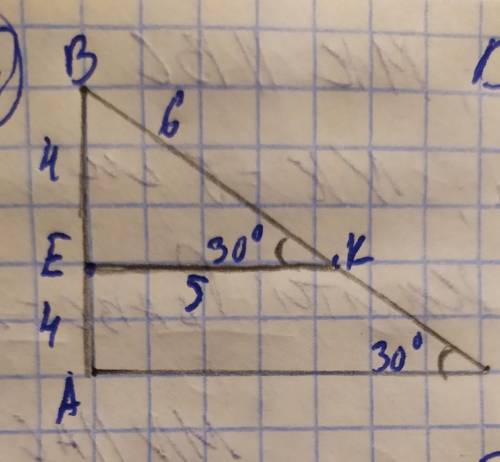
Дано: треугольник ABC; E-середина AB , BE = 4 см BK= 6 см, EA = 4см , угол BKE = 30 градусов, угол C = 30 градусов найти: BC и AC -?​

Хорошо, давайте решим эту задачу поэтапно.

1. Возьмем аксиомы геометрии:
- Серединный перпендикуляр к отрезку делит его на две равные части.
- В равнобедренном треугольнике биссектриса угла делит противолежащую сторону на две равные части.
- Сумма углов треугольника равна 180 градусам.

2. Из задания известно:
- BE = 4 см (это сторона, равняющаяся половине стороны AB).
- BK = 6 см (это половина стороны AB).
- EA = 4 см (это сторона, равняющаяся половине стороны AB).
- Угол BKE = 30 градусов.
- Угол C = 30 градусов.

3. Нам необходимо найти стороны BC и AC.

4. Обратим внимание, что треугольник BKE является прямоугольным треугольником (из-за свойств серединного перпендикуляра). Также, угол B равен 90 градусов.

5. Используя свойства прямоугольного треугольника, мы можем найти длину стороны KE с помощью теоремы Пифагора: KE^2 = BK^2 + BE^2. Подставим известные значения: KE^2 = 6^2 + 4^2 = 36 + 16 = 52. Возьмем квадратный корень из обеих частей: KE = √52 = 2√13 см.

6. Также, мы можем найти длину стороны BK, зная, что BK = 6 см.

7. Поскольку BE = EA, то треугольник AKE является равнобедренным треугольником. Аналогично, мы можем найти длину стороны AK, зная, что AK = 4 см.

8. Далее, мы можем поделить треугольник AKC на два равнобедренных треугольника AKE и CKH (H - точка на отрезке AC, которая делит его пополам).

9. Так как угол C равен 30 градусам, то угол KCH также равен 30 градусов (из-за равенства углов треугольника AKC).

10. Используя свойства равнобедренного треугольника, мы можем найти длину стороны CK = CH.

11. Далее, мы можем найти длину отрезка AH (лучше измерить на рисунке, если возможно), используя теорему Пифагора и стороны CK и KE.

12. И, наконец, мы получаем BC как сумму CK и AH, а AC как сумму BC и BK.

Таким образом, указанные шаги позволяют нам найти искомые стороны треугольника BC и AC.