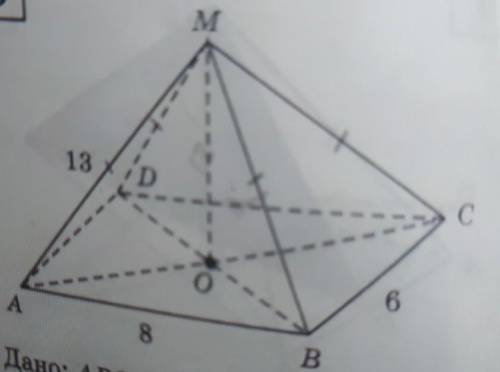
Дано прямоугольник ABCD Найдите расстояние от точки M до плоскости ABCD
чень

Чтобы найти расстояние от точки M до плоскости ABCD, мы можем использовать формулу для вычисления расстояния от точки до плоскости. Формула состоит из нескольких шагов:

Шаг 1: Найдите вектор нормали к плоскости ABCD.
Вектор нормали может быть найден путем нахождения косинуса угла между нормалью и любым вектором в плоскости.

Для прямоугольника ABCD, мы можем взять два вектора: AB и AD. Затем мы вычисляем их векторное произведение, чтобы получить вектор нормали к плоскости ABCD.

Вектор AB = B - A = (4 - 1) i + (0 - 0) j + (0 - 0) k = 3i
Вектор AD = D - A = (1 - 1) i + (4 - 0) j + (0 - 0) k = 4j

Теперь мы вычисляем векторное произведение AB x AD:
AB x AD = (3i) x (4j) = 12k

Таким образом, вектор нормали к плоскости ABCD равен 12k.

Шаг 2: Найдите уравнение плоскости ABCD.
Когда у нас есть вектор нормали, мы можем использовать одну из точек плоскости ABCD для построения уравнения плоскости. Для простоты мы можем использовать точку A(1, 0, 0):

x - x₀ y - y₀ z - z₀
------- + ------- + ------- = 0
3 0 12

где x₀, y₀ и z₀ - координаты точки A.

Теперь у нас есть уравнение плоскости ABCD.

Шаг 3: Найдите уравнение прямой, проходящей через точку M и перпендикулярной плоскости ABCD.
Уравнение прямой, перпендикулярной плоскости ABCD, будет иметь следующий вид:

x - x₁ y - y₁ z - z₁
------- = ------- = -------
12 0 0

где x₁, y₁ и z₁ - координаты точки M.

Шаг 4: Найдите пересечение прямой и плоскости.
Теперь у нас есть два уравнения: уравнение плоскости ABCD и уравнение прямой, перпендикулярной плоскости ABCD. Подставим одно уравнение в другое, чтобы найти точку пересечения:

x - 1 y z
------ + ------ + ----- = 0
3 0 12

x - x₁ y - y₁ z - z₁
------- = ------- = -------
12 0 0

Подставим уравнение прямой в уравнение плоскости:
(x₁ - 1) / 3 = (y₁ - 0) / 0 = (z₁ - 0) / 12

Из уравнения (x₁ - 1) / 3 = (z₁ - 0) / 12 мы можем решить относительно x₁:
(x₁ - 1) / 3 = (z₁ - 0) / 12
12(x₁ - 1) = 3(z₁ - 0)
12x₁ - 12 = 3z₁
12x₁ - 3z₁ = 12

Из уравнения (x₁ - 1) / 3 = (y₁ - 0) / 0 мы можем увидеть, что знаменатель равен 0, следовательно, y₁ = 0.

Теперь у нас есть система уравнений:
12x₁ - 3z₁ = 12
y₁ = 0

Для простоты мы можем решить первое уравнение относительно z₁:
12x₁ - 3z₁ = 12
-3z₁ = 12 - 12x₁
z₁ = 4 - 4x₁

Таким образом, мы получили выражение для z₁ в зависимости от x₁.

Шаг 5: Найдите расстояние от точки M до плоскости ABCD.
Расстояние от точки M до плоскости ABCD будет равно расстоянию от точки M до найденной точки пересечения. Для этого нужно использовать формулу для вычисления расстояния между двумя точками:

d = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²)

где (x₁, y₁, z₁) - координаты точки M, (x₂, y₂, z₂) - координаты точки пересечения.

В нашем случае точка M имеет координаты M(2, 0, 5), а координаты точки пересечения являются переменными x₁ и z₁.

Подставим все значения:
d = √((x₂ - 2)² + (y₂ - 0)² + (z₂ - 5)²)

Теперь нужно найти значения x₂ и z₂. Мы можем подставить выражение для z₁ в зависимости от x₁ в уравнение плоскости ABCD, чтобы получить выражение для x₂:

x - x₀ y - y₀ z - z₀
------- + ------- + ------- = 0
3 0 12

(x₂ - 1) / 3 + 0 + (z₂ - 0) / 12 = 0
(x₂ - 1) / 3 + z₂ / 12 = 0

(x₂ - 1) / 3 = - z₂ / 12
x₂ - 1 = -3z₂ / 12
x₂ = 1 - 3z₂ / 12
x₂ = 1 - z₂ / 4

Теперь у нас есть выражение для x₂ в зависимости от z₂.

Подставим это выражение в формулу для расстояния:
d = √(((1 - z₂ / 4) - 2)² + (0 - 0)² + (z₂ - 5)²)

Упростим это выражение:
d = √((1 - z₂ / 4 - 2)² + (z₂ - 5)²)
d = √((-1 - z₂ / 4)² + (z₂ - 5)²)
d = √((1 + z₂ / 4)² + (z₂ - 5)²)
d = √(1 + 2z₂ / 4 + z₂² / 16 + z₂² - 10z₂ + 25)

Теперь нам нужно найти минимальное значение для этого уравнения, чтобы найти расстояние от точки M до плоскости ABCD. Для этого нужно найти производную этого уравнения по z₂ и приравнять его к нулю:

d' = 0
(2z₂ / 4 + 2z₂ - 10) / 2√(1 + 2z₂ / 4 + z₂² / 16 + z₂² - 10z₂ + 25) = 0

Раскроем скобки и упростим это уравнение:
(2z₂ + 8z₂ - 20) / 4√(16 + 8z₂ + 16z₂² - 40z₂ + 100) = 0
(10z₂ - 20) / 4√(16 + 8z₂ + 16z₂² - 40z₂ + 100) = 0
10z₂ - 20 = 0
10z₂ = 20
z₂ = 2

Теперь найдем x₂, подставив z₂ = 2 в уравнение x₂ = 1 - z₂ / 4:
x₂ = 1 - 2 / 4 = 1 - 1/2 = 1/2
x₂ = 1/2

Таким образом, координаты точки пересечения равны M'(1/2, 0, 2).

Теперь, используя формулу для вычисления расстояния между двумя точками:
d = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²)
d = √((1/2 - 2)² + (0 - 0)² + (2 - 5)²)
d = √((-3/2)² + 9)
d = √(9/4 + 9)
d = √(9/4 + 36/4)
d = √(45/4)
d = √(45) / √(4)
d = √(9 * 5) / 2
d = 3√5 / 2

Таким образом, расстояние от точки M до плоскости ABCD равно 3√5 / 2.