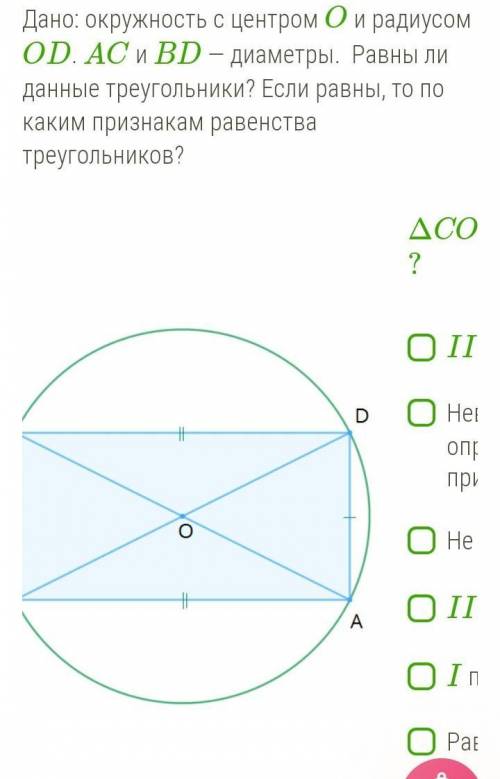
Дано: окружность с центром O и радиусом OD. AC и BD — диаметры. Равны ли данные треугольники? Если равны, то по каким признакам равенства треугольников?
Ответы
Для начала давайте разберемся, что такое треугольник. Треугольник - это геометрическая фигура, состоящая из трех отрезков, называемых сторонами, и трех вершин, где стороны соединяются. Теперь посмотрим на изображение.
Мы видим два треугольника: треугольник AOC и треугольник BOD. Давайте посмотрим на свойства данных треугольников, чтобы узнать, равны они или нет.
Сначала обратим внимание на стороны треугольников. Сторона AC соединяет вершины A и C, а сторона BD соединяет вершины B и D. При этом точка O является центром окружности, от которой проведены диаметры AC и BD. Важно заметить, что для обоих треугольников стороны AC и BD равны, так как это диаметры окружности.
Теперь обратим внимание на углы треугольников. В треугольнике AOC у нас есть два угла: угол AOC и угол OAC. А в треугольнике BOD у нас также имеются два угла: угол BOD и угол OBD. Если окружность и ее диаметры равны, то углы при основании диаметров должны быть прямыми. Это означает, что у нас есть два прямых угла в каждом из треугольников.
Таким образом, мы видим, что у треугольников AOC и BOD равные стороны (AC и BD) и равные углы при основании диаметров (углы AOC и BOD). Поэтому данные треугольники равны, так как выполняются все условия равенства треугольников.
Вывод: треугольники AOC и BOD равны по признакам равных сторон (AC и BD) и признакам равных углов при основании диаметров (углы AOC и BOD).
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Сочинение рассуждение объясните как понимаете смысл финала текста саню распирало...
2 - Напишите рассказ о себе (10-20 строчек)...
3 - Напишите эссе по экологии 9 класс на тему я с тобой природа одной крови...
3 - 15 из восьми последовательных чисел сумма некоторых семи равна 815. найдите восьмое...
3 - Царевна лягушка составить план выполнение царских...
3 - Укузнеца был запас подков ,а когда он сделал ещё три,то смог подковать 17 лошадей....
3 - Как сделать морфологический разбор слово износилась подскажите мне ! (...
2 - Вкаком году произошло освобождение руси от ордынского ига ?...
3 - Твір про гусеницю ключові слова: гусениця,невеличка,листок гала,комахи,ні голосу,ні...
1 - Деревни асква, бсква, всква и гсква находятся на одном прямом шоссе, но в каком...
3