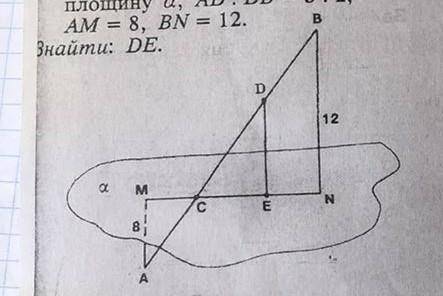
дано: mn проекція відрізка ab на площину альфа AD:DB = 3:2. AM= 8 BN=12.Знайти:DE​

Для решения данной задачи, давайте использовать соотношение между проекциями отрезков на плоскость альфа.

Из условия задачи нам дано, что проекция отрезка AB на плоскость альфа имеет отношение AD:DB = 3:2.

Давайте рассмотрим треугольник ADM на рисунке. Из условия задачи, известны значения AM = 8 и BN = 12, поэтому мы можем вычислить все остальные стороны треугольника.

1. Сначала найдем сторону DM. Поскольку AM является высотой треугольника ADM, а DM - основанием этой высоты, мы можем воспользоваться формулой для площади треугольника:

Площадь треугольника ADM = (1/2) * DM * AM

Из формулы площади треугольника также следует, что площадь треугольника ADM может быть представлена и как произведение половины основания треугольника на его высоту, то есть площадь треугольника ADM = (1/2) * AB * DN.

Из этого следует, что (1/2) * DM * AM = (1/2) * AB * DN

Подставляя известные значения AM = 8 и DN = 3, получаем:

(1/2) * DM * 8 = (1/2) * AB * 3

Упрощая уравнение, получаем:

4DM = AB * 3

2. Теперь найдем сторону AB. Так как AB - диагональ прямоугольного треугольника AMN, мы можем воспользоваться теоремой Пифагора:

AB^2 = AM^2 + BN^2

Подставляя известные значения AM = 8 и BN = 12, получаем:

AB^2 = 8^2 + 12^2
AB^2 = 64 + 144
AB^2 = 208

3. Используя полученное значение AB^2 = 208 из пункта 2, подставим его в уравнение из пункта 1:

4DM = AB * 3
4DM = √208 * 3

Упрощая уравнение, получаем:

DM = (√208 * 3) / 4
DM = (√208 * 3) / 2^2
DM = (√208 / 2) * (3 / 2)

4. Теперь найдем сторону DE. Из треугольника DME следует:

DE^2 = DM^2 + ME^2

Подставляя DM = (√208 / 2) * (3 / 2), вычислим значение DE:

DE^2 = [(√208 / 2) * (3 / 2)]^2 + ME^2

Упрощая уравнение, получаем:

DE^2 = 9/16 * 208 + ME^2

5. Выражаем значение ME^2:

ME^2 = DE^2 - 9/16 * 208

6. Теперь найдем сторону EN. Так как BN - высота треугольника EBN, а EN - основание высоты, мы можем использовать аналогичные соотношения для площадей:

Площадь треугольника EBN = (1/2) * EN * BN

Но также, площадь треугольника EBN равна произведению половины основания на высоту, то есть

Площадь треугольника EBN = (1/2) * AB * ME

Подставляя известные значения AB = √208 и ME^2 (полученное в пункте 5), получаем:

(1/2) * EN * 12 = (1/2) * √208 * √(DE^2 - 9/16 * 208)

Упрощая уравнение, получаем:

EN * 12 = √208 * √(DE^2 - 9/16 * 208)

Теперь выразим значение EN:

EN = (√208 * √(DE^2 - 9/16 * 208)) / 12

7. Мы можем заметить, что сторона DN является разностью сторон EN и DM:

DN = EN - DM

Подставляя полученные значения EN и DM, получаем:

DN = [(√208 * √(DE^2 - 9/16 * 208)) / 12] - [(√208 / 2) * (3 / 2)]

Таким образом, мы решили задачу и вычислили значение стороны DN в зависимости от стороны DE. Если вам нужна еще какая-то информация или объяснение, пожалуйста, сообщите мне.