Дано: куб АВСDA1B1C1D1, 0 - центр грани ABCD куба, ребро куба 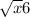 Найти: ОА1 - расстояние от точки О до одной из вершин куба
Найти: ОА1 - расстояние от точки О до одной из вершин куба
С объяснениями
Другие вопросы по теме Геометрия
Популярные вопросы
- Декартовы координаты в пространстве...
3 - У рівнобічній трапеції бічна сторона дорівнює 22 см, а кут між висотою,...
1 - Вычисли периметр треугольника ABC и сторону BA, если CF — медиана, BC=CA=150мм...
1 - Назвать соединение и зарисовать к нему структурную формулу изомера и гомолога....
3 - Выполните упражнение 86, стр. 46 Спишите, обозначьте суффиксы причастий....
2 - Найти ты приближение значение функции в данных точках у=x⁶, x=2,01...
3 - Написать программу определения стоимости разговора по телефону с учетом...
3 - З кількох частин складається енеїда котляревського...
2 - яка маса осаду утвориться під час взаємодії розчину алюміній хлориду з 220...
3 - В один из двух одинаковых кусочков пластилина спрятан металический предмет...
1
Итак, давайте начнем:
1. Рассмотрим треугольник ОА1C1. В этом треугольнике сторона ОС квадрата ABCD является гипотенузой, сторона ОА1 - катетом, а сторона C1А1 - другим катетом.
2. Мы уже знаем, что ребро куба равно
3. Поскольку точка О является центром грани ABCD, то точка С1 - середина стороны А1Б1. Из этого следует, что длина стороны C1А1 равна половине длины стороны А1Б1, то есть
4. Теперь мы можем найти длину стороны ОА1, используя теорему Пифагора:
ОА1² = ОС² - C1А1²
Подставим известные значения:
ОА1² = (
ОА1² =
ОА1² =
5. Приравняем ОА1² к расстоянию ОА1, чтобы найти значение ОА1:
ОА1 =
Таким образом, расстояние от точки О до одной из вершин куба равно