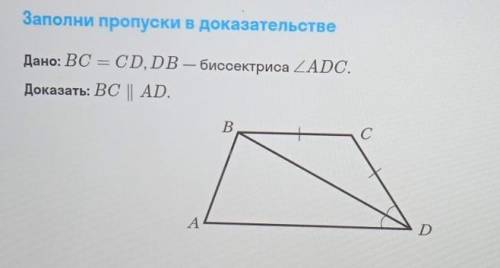
Дано: BC = CD, DB — биссектриса ADC.
Доказать: BC || AD.​

Чтобы доказать, что BC || AD, нам нужно найти основание DB и проверить его соотношение с отрезками BC и CD.

Дано, что BC = CD, это значит, что сторона BC и сторона CD равны между собой.

Также дано, что DB - это биссектриса ADC. Биссектриса разделяет угол на две равные части. В нашем случае, DB делит угол ADC на два равных угла.

Рассмотрим треугольник DBC. По условию, BC = CD, и угол DBC равен углу DCB (так как DB - это биссектриса). Таким образом, треугольник DBC является равнобедренным треугольником, в котором сторона BC равна стороне CD, а угол DBC равен углу DCB.

Теперь рассмотрим треугольник ADC. У нас уже есть равенство сторон BC = CD, и по условию угол DBC равен углу DCB. Вместе это означает, что треугольник DBC и треугольник ADC подобны (по признаку SSS).

По свойству подобных треугольников, соответственные стороны параллельны. То есть, сторона AD параллельна стороне BC (так как AD соответствует стороне BC), или можно сказать, что BC || AD.

Таким образом, мы доказали, что BC || AD, используя свойство сходства подобных треугольников и условия задачи.