Дано: АВ = 3 ВС = 4 СС1 = 12
Найти длину вектора АС1
Другие вопросы по теме Геометрия
Популярные вопросы
- Какая главная мысль у белого пуделя...
2 - Спиши текст, ответь на вопросы, добавив предложение - ответ на последний...
1 - Требуется изготовить реостат на 20 ом из никелиновой проволоки площадью...
3 - Какая масса алюминиевого порошка потребуется для полного восстановления...
1 - Плотность населения в а)россии.б) симферополе...
2 - Периметр равносторонего треугольника равен 21см.из двух таких треугольников...
2 - Раскройте скобки и а) х-(х-(3х-1)) б) 5а-(6а-(7а-(8а-...
1 - изображения пространства с точками схода на горизонте?...
1 - Твыр на тему для чого ми вивчаэмо рыдну мову...
2 - Слова очумелова о хрюкине и щенке в рассказе хамелеон ....
2
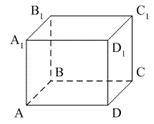
Для начала, обратимся к картинке. Мы видим, что треугольник AC1S1 является прямоугольным, так как угол ASC1 равен 90 градусов. Для нахождения длины вектора АС1, нам необходимо найти длины векторов АВ и ВС1, а затем применить теорему Пифагора.
Из задачи нам дано, что АВ = 3, ВС = 4 и СС1 = 12.
Шаг 1: Найдем длину вектора АС1.
Для этого, сначала найдем длину вектора АС. Для этого сложим длины векторов АВ и ВС:
АС = АВ + ВС
АС = 3 + 4
АС = 7
Шаг 2: Найдем длину вектора С1С. Для этого вычтем из длины вектора АС1 длину вектора СС1:
С1С = АС1 - СС1
С1С = 7 - 12
С1С = -5 (отрицательный результат)
Теперь, применяя теорему Пифагора, найдем длину вектора АС1:
АС1 = √(С1С^2 + СС1^2)
АС1 = √((-5)^2 + 12^2)
АС1 = √(25 + 144)
АС1 = √169
АС1 = 13
Таким образом, длина вектора АС1 равна 13.