. Дано: АC = BD, угол OCD = углу ODC.
Доказать: ΔAСD = ΔBCD.
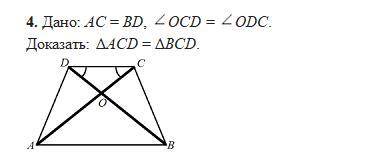
Другие вопросы по теме Геометрия
Популярные вопросы
- Выпишите деепричастия и пояснеямые ими глаголы : дельфины посапывая кувыркались...
2 - Из пункта м в пункт n, расстояние между которыми 18км, вышли одновременно...
3 - Найдите длину отрезка км (в единичных отрезках) если к(-12),м(-8)...
2 - Лодка проплыла расстояние между пристанями вниз по течению реки и вернулась...
1 - 1) 15xy^3/10x^3y= 2) ab-b/b^2= 3)4x^2-xy^2/2x-y=...
1 - Cтепень окисления всех элементов tioso4...
3 - 1)за одну неделю в санатории израсходовали 28 кг картошки.сколько кг картошки...
2 - Одну спросили сколько ей лет? она ответила без субот и воскресений. сколько...
3 - Write a tag for each sech sentence. 1.you dont know his 2.you know her...
3 - Випишіть з орфографічного словника 5 прислівників утворених за аби-,ані-,де-,чи-,що-,як-....
1
Доказать: ΔAСD = ΔBCD.
Для доказательства равенства треугольников АСД и ВСД, мы можем использовать две стороны и угол между ними.
Шаг 1: Из дано AC = BD.
Используя данный факт, мы можем заметить, что сторона АС для треугольника АСД равна стороне BD для треугольника ВСД.
Шаг 2: Из дано угол OCD = углу ODC.
Это означает, что углы COD и ODC равны между собой.
Шаг 3: Теперь мы можем использовать эти данные, чтобы показать, что треугольники АСД и ВСД равны друг другу.
Возьмем первый треугольник АСД:
Сторона АС равна стороне BD (из шага 1).
Угол COD равен углу ODC (из шага 2).
Сторона АD общая для обоих треугольников.
Таким образом, у нас есть два одинаковых угла и одна общая сторона, что означает, что треугольники АСД и ВСД равны (по признаку равенства треугольников SSS).
Итак, мы доказали, что ΔAСД = ΔВСД, основываясь на данных AC = BD и угол OCD = углу ODC.