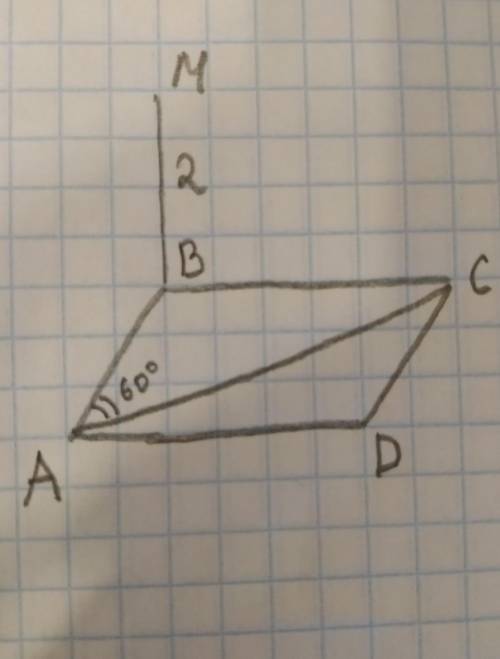
Дано: ABCD — прямоугольник, ZBAC = 60°,
MBI (ABCD), MB = 2, расстояние от точки M до
прямой AD равно 8.
Найти: расстояние от точки M до прямой АС.​

Для решения данной задачи, нужно воспользоваться сведением о равнобедренных треугольниках и прямоугольниках.

Из условия задачи мы знаем, что ABCD - прямоугольник, ZBAC = 60°, MB = 2 и расстояние от точки M до прямой AD равно 8.

Для начала, обратим внимание на треугольник MBD. Мы знаем, что MB = 2 и расстояние от точки M до прямой AD равно 8. Поскольку ADC - прямоугольник, то BC || AD и высота M d1 к стороне BD является медианой и, следовательно, перпендикулярна к стороне BD.

Таким образом, в треугольнике MBD у нас есть прямой треугольник, в котором известны катеты MB и d1, а искомое — расстояние от точки M до прямой AD (здесь обозначено как d2). Нам нужно найти эту третью сторону M d2.

Мы можем воспользоваться теоремой Пифагора для нахождения стороны hypotenuse в прямоугольном треугольнике. Она гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Таким образом, мы можем записать уравнение:
(2)^2 + (d1)^2 = (d2)^2.

Теперь нам нужно определить значение d1. Мы знаем, что треугольник ABC - равнобедренный с углом BAC = 60°. В равнобедренном треугольнике медиана из вершины, образующая угол с основанием равным 60°, делит этот угол пополам. Таким образом, в восходящем угле ABC имеем угол 60°, а в углу BAC - 30°.

Теперь мы можем рассмотреть треугольник ZBM. Угол BZM равен 30° (60° : 2). Мы знаем длину стороны MB, поскольку MB = 2 и теперь можем использовать тригонометрические отношения для нахождения длины стороны BM.

В данном случае нам пригодится функция синуса, поскольку из угла имеется противолежащая и гипотенуза (у нас есть угол BZM и гипотенуза BM).
Таким образом, мы можем записать уравнение: sin(30°) = (d1) / 2.

Из этого уравнения можем найти длину d1:
d1 = 2 * sin(30°).

Теперь, мы можем вернуться к нашему уравнению для треугольника MBD:
(2)^2 + ((2 * sin(30°))^2) = (d2)^2.

Перейдем к решению данного уравнения:
4 + 4 * (1/2)^2 = (d2)^2.
4 + 4 * (1/4) = (d2)^2.
4 + 1 = (d2)^2.
5 = (d2)^2.

Чтобы найти d2, возьмем квадратный корень с обеих сторон:
√(5) = d2.

Таким образом, расстояние от точки M до прямой АС равно √(5) или 2.24 (округляя до двух десятичных знаков).