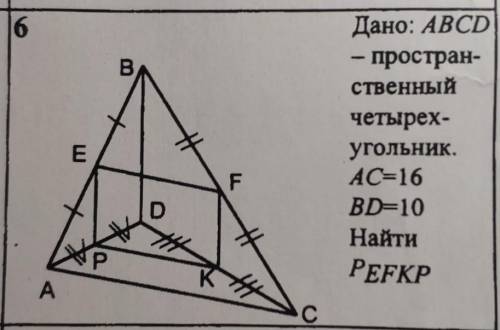
Дано: ABCD - пространственный четырехугольник. AC = 16, BC = 10. Найти P(EFKP)
Ответы
Чтобы найти периметр четырехугольника EFKP, нам нужно найти длину каждой его стороны и сложить их вместе.
Заданы стороны AC = 16 и BC = 10. Давайте сначала найдем сторону FK.
Обратите внимание на треугольники ACF и BCF. Оба эти треугольника являются прямоугольными, так как их боковые стороны параллельны и перпендикулярны друг к другу.
В треугольнике ACF, известны гипотенуза AC = 16 и один катет CF (длина стороны BC = 10). Используем теорему Пифагора, чтобы найти длину другого катета AF:
AF^2 = AC^2 - CF^2
AF^2 = 16^2 - 10^2
AF^2 = 256 - 100
AF^2 = 156
AF = sqrt(156)
AF ≈ 12.49
Теперь, чтобы найти сторону FK, вычитаем длину стороны AF из длины стороны AC:
FK = AC - AF
FK = 16 - 12.49
FK ≈ 3.51
Теперь у нас есть длины сторон FK и KP равные 3.51. Чтобы найти длину стороны EF, нам нужно найти длину BF, а затем вычесть ее из длины стороны EK.
В треугольнике BCF, известны гипотенуза BC = 10 и один катет CF (длина стороны AC = 16). Используя теорему Пифагора, мы находим длину другого катета BF:
BF^2 = BC^2 - CF^2
BF^2 = 10^2 - 16^2
BF^2 = 100 - 256
BF^2 = -156
Здесь мы столкнулись с проблемой. Значение -156 означает, что значение под корнем является отрицательным, что невозможно для длины стороны. Возможно, существует ошибка в постановке задачи или рисунке.
Таким образом, мы не можем найти длину стороны EF и, следовательно, не можем найти периметр четырехугольника EFKP.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Итоги развития Республики Беларусь как суверенного государства Урок обобщения:...
3 - : Чим мене зворушує образ Соломії (твір Дорогою ціною) даю 100 б...
3 - Свойства ГО …………………………………………. В чем суть данного свойства ГО Пример проявления...
1 - Коло, вписане в трикутник MPN, дотикається до сторони MN в точці С, такій, що...
1 - очень надо:( ЗАВДАННЯ №2 Запишіть прислів’я. Підкресліть в кожному реченні дієприкметниковий...
3 - , только нужно объяснение и все формулы сторона квадрата дорівнює 5√2 знайдіть...
2 - Усі ребра правильного тетраедра SABC дорівнюють корінь з 3. Точка K є серединою...
2 - Дода sale657Запишите предложения, изменив их так, чтобы они соответство-вали...
1 - Английский 10 класс конструкция if...
2 - Кто сделает ещё скину 10грн на карту !...
3