Дано: ABCD - параллелограмм, BD перпендикулярна альфа, AB=7. Найти периметр ABCD.
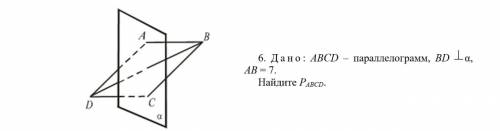
Другие вопросы по теме Геометрия
Популярные вопросы
- визначте напругу на ділянці електричного кола, якщо її опір становить...
1 - расчитать количество продуктов необходимое для приготовления...
1 - Составьте два предложения с наречиями ...
2 - Эта удивительная история началась в кон- це 1941 года, когда...
1 - 1.Дайте визначення хайку,назвіть його провідні ознаки,відомого...
1 - Островский Снегурочка . в какое время года происходят события...
3 - Найдите в предложениях обособленные члены. Определите, чем они...
1 - 1116. 2) Морская вода содержит 5% воды, остальное - соль. Сколь-ко...
2 - 11-тапсырма. Орбита жолының 1-тапсырмасын орындаңдар. 1. Гиннестің...
1 - Химия решить , сдесь нужно вести соответствии...
2
Точки А и С лежат в альфа, следовательно, альфа пересекает паралл-гр по прямой АС. BD перпендикулярна альфа, следовательно, BD перпендикулярна AC. Тогда ABCD - ромб, и его периметр равен 4*7 = 28 см.
Объяснение:
Во-первых, по определению параллелограмма противоположные стороны равны, то есть AB = CD и AD = BC.
Во-вторых, так как BD перпендикулярна альфа (пусть это будет угол BAD), то мы можем использовать теорему Пифагора в треугольнике ABD, чтобы найти длину AD.
Таким образом, имеем следующие данные:
AB = 7 (дано)
AB = CD (свойство параллелограмма)
AD = BC (свойство параллелограмма)
Для решения задачи нам необходимо найти периметр ABCD, то есть сумму всех его сторон.
1. Найдем длину стороны AD:
Используя теорему Пифагора в треугольнике ABD, получаем:
AB^2 + AD^2 = BD^2
7^2 + AD^2 = BD^2
49 + AD^2 = BD^2
2. Так как BD перпендикулярна альфа, то у нас есть прямоугольный треугольник BDA. По свойству прямоугольного треугольника, где BD - гипотенуза, AD - катет, альфа - прямой угол, то у нас есть теорема Пифагора.
BD^2 = AD^2 + AB^2
AD^2 = BD^2 - AB^2
AD^2 = BD^2 - 49
3. Так как AD = BC, то и BC^2 = BD^2 - 49
4. Поскольку AB = CD, то и AD = BC
Из уравнения AD^2 = BD^2 - 49 следует, что BC^2 = BD^2 - 49
5. С помощью квадратного корня найдем значение BC:
BC = √(BD^2 - 49)
Так как BD - гипотенуза треугольника BDA, то BD^2 = AD^2 + AB^2 = AD^2 + 49
Подставляем это значение в уравнение:
BC = √((AD^2 + 49) - 49)
BC = √(AD^2)
BC = AD
Теперь у нас есть все стороны параллелограмма ABCD:
AB = CD = 7
AD = BC = √(AD^2)
Суммируем все стороны, чтобы найти периметр:
Периметр ABCD = AB + BC + CD + AD
Периметр ABCD = 7 + √(AD^2) + 7 + √(AD^2)
Периметр ABCD = 14 + 2√(AD^2)
6. Ответом будет уравнение с подставленным значением AD:
Периметр ABCD = 14 + 2√(AD^2)
Таким образом, чтобы найти периметр ABCD, нам необходимо найти значение AD с помощью уравнения AD^2 = BD^2 - 49 и затем подставить это значение в выражение для периметра ABCD.