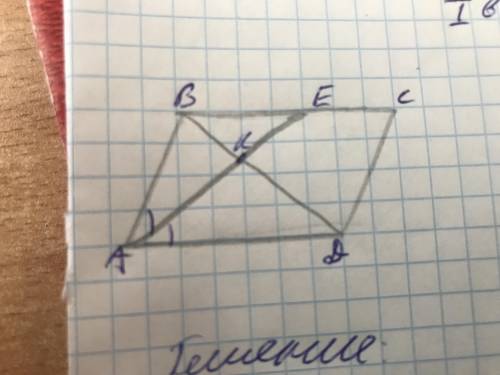
Дано: abcd параллелограмм
Ae биссектриса
Ab:bc = 4:9
Найти bk/kd

Чтобы найти значение bk/kd, нам нужно разобраться с данными, которые уже известны:

1. В задаче указано, что abcd является параллелограммом. Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны и равны.

2. Ae – биссектриса угла abd. Биссектриса – это луч, который делит угол на два равных угла. В данном случае он делит угол abd на два равных угла (абсолютные величины углов равны).

3. Ab:bc = 4:9. Это отношение указывает на то, что отрезок Ab является 4/9 частью отрезка bc.

Теперь перейдем к решению задачи:

1. Обратим внимание на симметричность параллелограмма: сторона Ab параллельна стороне cd, и сторона bc параллельна стороне ad.

2. Также обратим внимание на свойство биссектрисы Ae: она делит угол abd на два равных угла.

3. Поскольку abcd – параллелограмм, угол abd и угол bcd – смежные углы и они дополняют друг друга до 180 градусов (AB II CD, значит угол abd = угол bcd).

4. Пусть bk и kd – это отрезки b и d (соответственно) на стороне bc, причем bk обозначает отрезок между точками b и e, а kd – отрезок между точками e и d.

5. Отрезок bk равен (4/9) * bc, а отрезок kd равен (5/9) * bc. Мы получили эти значения, так как отношение Ab:bc равно 4:9, а cd и bc являются симметричными сторонами к ab и bc соответственно.

6. Искомая величина bk/kd представляет собой отношение отрезка bk к отрезку kd, то есть (4/9) * bc / (5/9) * bc. Большинство частей в этих отношениях сокращаются, и остается только 4/5.

Ответ: bk/kd = 4/5