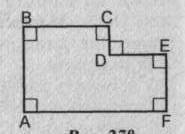
Дано: AB=BC=3, AF=5, EF=2
Найти: S abcdef

Объяснение:

делим эту сложную фигуру на 2е простые

получается продублируем сторону ЕF

найдем площади по отдельности

фигуры АВСF` и DF`FE

и просумируем получим площадь целой фигуры

Sabcf`= AB×BC= 3×3=9

F`F= AF-BC=5-3=2

Sdf`fe=EF×FF`=2×2=4

Sabcdef=Sabcf`+Sdf`fe=4+9=13

Чтобы найти площадь фигуры ABCDEF, нужно разделить её на несколько более простых фигур, для которых мы знаем формулы вычисления площади.

Дано:

AB=BC=3 - это означает, что отрезки AB и BC имеют одинаковую длину, равную 3.
AF=5 - отрезок AF имеет длину 5.
EF=2 - отрезок EF имеет длину 2.

Первым шагом, нам нужно разделить фигуру ABCDEF на два треугольника. Мы видим, что треугольники ABF и BCF являются равнобедренными, поскольку AB=BC.

Теперь, мы можем найти площадь каждого из этих треугольников, используя формулу для площади равнобедренного треугольника: S = (основание * высота) / 2.

Для треугольника ABF:
основание = AB = 3
высота = EF + AF = 2 + 5 = 7

S(abf) = (3 * 7) / 2 = 21 / 2 = 10.5

Для треугольника BCF:
основание = BC = 3
высота = EF + AF = 2 + 5 = 7

S(bcf) = (3 * 7) / 2 = 21 / 2 = 10.5

Теперь нам нужно найти площадь четырехугольника BCEF. Мы замечаем, что этот четырехугольник можно разделить на два треугольника CEF и BCF и прямоугольник BCDE.

Площадь прямоугольника BCDE можно найти, используя формулу S = длина * ширина:
длина = AB = 3
ширина = EF = 2

S(bcde) = 3 * 2 = 6

Площадь треугольника CEF мы уже вычислили в предыдущем шаге:
S(cef) = 10.5

Итак, площадь четырехугольника BCEF равна сумме площадей треугольника CEF и прямоугольника BCDE:
S(bcef) = S(cef) + S(bcde) = 10.5 + 6 = 16.5

И, наконец, чтобы найти площадь всей фигуры ABCDEF, нужно сложить площади треугольников ABF и BCEF:
S(abcdef) = S(abf) + S(bcef) = 10.5 + 16.5 = 27.

Таким образом, площадь фигуры ABCDEF составляет 27 квадратных единиц.