1. Геометрия
  2. Дано: AB||A1B1, AK-биссектриса

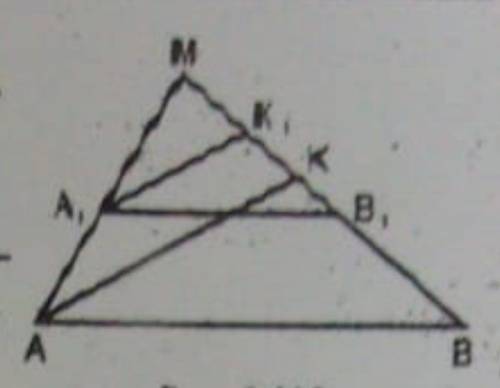
Дано: AB||A1B1, AK-биссектриса угла MAB, A1K1-биссектрисса MA1B1 Доказать: угол MA1K= углу MAK. могут ли быть паралельными прямые A1K1 и AK


Дано: AB||A1B1, AK-биссектриса угла MAB, A1K1-биссектрисса MA1B1 Доказать: угол MA1K= углу MAK. могу

Lily566 Lily566    2   02.02.2021 18:38    90

Ответы
sebtetfGек5у sebtetfGек5у  02.02.2021 18:40
много ! с решением
Предыдущий
Следующий
Задай вопрос
Неограниченные возможности для обучения без рекламы со Знаниями Плюс
ПОКАЗАТЬ ОТВЕТЫ
cheropitan cheropitan  02.02.2021 18:40

∠МА1К1 = ∠МАК, т.к. А1В1 || АВ, значит

∠МА1К1 = ∠МАК, т.к. А1К1 и АК — биссектрисы равных углов Прямые АК и A1K1 не могут пересекаться, т.к. они параллельны, г к соответственные углы равны.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
kamillionela kamillionela  13.05.2020 11:18
Використовуючи скалярний добуток двох векторів в трикутнику ABC з координатами вершин A (1;0) B (-2;4) C (2;0) знайдіть cos A​...
умник1235678 умник1235678  13.05.2020 11:18
В равнобедренном треугольнике АВС с основанием AC отрезок ВЕ-высота. Найдите угол ABC, если АЕ=4,2 см и угол ABЕ=24°...
PSerega11111111 PSerega11111111  13.05.2020 11:18
Кут ABC і кут A1B1C1 подібні. AB= 20 см, B1C1 = 15 см, AC = 40см, BC = 30 см. Знайдіть невидимі сторони кут A1B1C1. ​...
NikolayNik12 NikolayNik12  13.05.2020 11:17
8 класс. Геометрия. Прямоугольник MNFK вписан в окружность NM=3, MK=4. Найдите радиус окружности. Нужен чертеж...
Sijjj777 Sijjj777  13.05.2020 11:17
Мальчик построил две секущих так, как показано на рисунке, при этом образовался равнобедренный треугольник ВКО. ∠3 = 120°.​...
darkishlord darkishlord  13.05.2020 11:18
Решите задачу : Точки А (-4 ; -3) ; В ( -4 ; 5 ) ; С ( 2 ; 5 ) , Д ( 8 ; -3 ) - вершины прямоугольной трапеции с основаниями BC и АД . Найдите длину средней линии умираю...
annamacsimava08 annamacsimava08  31.05.2019 02:20
Апофема правильной треугольной пирамиды 4 см. радиус окружности описанной около основания см. найти площадь полной поверхности....
Marishka301 Marishka301  31.05.2019 02:20
Центр окружности, вписанной в равнобедренный треугольник abc с основаниями ас, делит высоту bm в отношении 17 делить на 15.найдите периметр и площадь треугольника, если...
Luchik22 Luchik22  15.01.2021 10:30
У трикутнику ABC sin A=0,2 , sin C=0,6 , BC= 3 см. Знайдіть AB....
kizaru28 kizaru28  15.01.2021 10:32
Високий рівень П.Відрізки АВ і МК перетинаються в точці 0, що є серединою відрізка MK,BM0 = AKO . Доведіть, що МОВ = КОА​пожайлуста пожайлуста...

Популярные вопросы