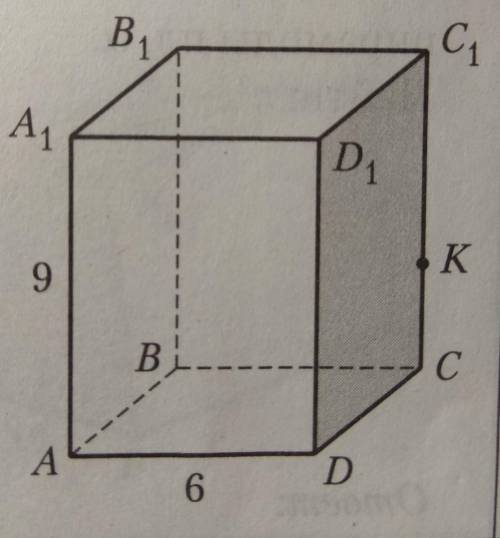
Дано: A...D1 - прямоугольный параллелепипед, CK : KC1 = 1 : 2. Периметр сечения параллелепипеда пл. ADK равен 22. Найти: Sбок параллелепипеда.​

Чтобы найти Sбок параллелепипеда, нам нужно знать высоту параллелепипеда, которую мы можем найти, зная периметр ADK.

Первым шагом, давайте найдем длину отрезка CD и DK. Поскольку CK : KC1 = 1 : 2, мы можем сказать, что CK составляет 1 часть от всего расстояния CK : (1 + 2 = 3) и KC1 составляет 2 части от всего расстояния CK : (1 + 2 = 3). Затем, мы можем найти длину отрезка KC, разделив CD на (1 + 2 = 3) части.

Длина отрезка CD является периметром сечения ADK, который равен 22. Значит, каждая часть CK составляет 22 / 3 = 7.33 (округлим до сотых).

Теперь мы можем найти длины отрезков CD и DK, учитывая, что CK : KC1 = 1 : 2. Длина CD равна CK + KC1, то есть 7.33 + 2 * 7.33 = 7.33 + 14.66 = 21.99 (округлим до сотых). Длина DK будет равна 2 * CK, то есть 2 * 7.33 = 14.66 (округлим до сотых).

Итак, мы нашли длины отрезков CD и DK: CD = 21.99 и DK = 14.66.

Теперь давайте найдем высоту параллелепипеда. Высота будет равна длине отрезка AD, так как AD является высотой параллелепипеда. Мы можем найти длину отрезка AD, используя теорему Пифагора в прямоугольном треугольнике ADK.

У нас уже есть одна сторона треугольника - это DK, равная 14.66. Мы знаем, что CK : KC1 = 1 : 2, так что KC1 будет равна половине DK, то есть 14.66 / 2 = 7.33.

Теперь мы можем применить теорему Пифагора: AD^2 = DK^2 + KC1^2. Подставляем известные значения: AD^2 = 14.66^2 + 7.33^2. Вычисляем: AD^2 = 214.9958 + 53.6489 = 268.6447. Поскольку мы ищем квадрат высоты, мы можем просто сказать, что AD = √268.6447 = 16.4 (округлим до десятых).

Таким образом, высота параллелепипеда AD равна 16.4.

Наконец, чтобы найти Sбок параллелепипеда, мы можем использовать формулу для площади боковой поверхности параллелепипеда. Формула: Sбок = 2(AD * (CD + DK)).

Подставляем значения: Sбок = 2(16.4 * (21.99 + 14.66)). Вычисляем: Sбок = 2(16.4 * 36.65) = 2 * 601.76 = 1203.52.

Таким образом, площадь боковой поверхности параллелепипеда Sбок равна 1203.52.