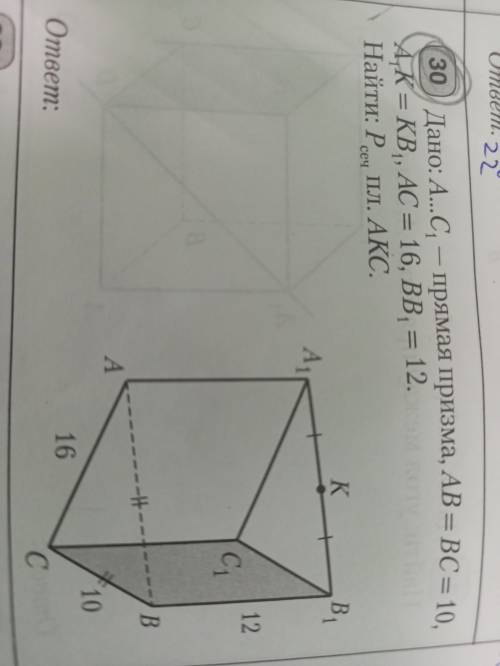
Дано:A...C1 - прямая призма ,AB = BC = 10, A1K = KB1, AC = 16 ,BB1 = 12 найти Pсеч. пл. AKC
Другие вопросы по теме Геометрия
Популярные вопросы
- Каковы размеры солнечной системы по сравнению с миром вселенной?...
3 - Перед обозначением номера столбца или строки в абсолютном адресе ячейки...
3 - Тело имеет вес 9кн определите его массу...
2 - Кнаименьшему общему знаменателю дроби 6\20 и 5\11; 11\24 и 1\30; 3\16...
3 - Найдите гипотенузу прямоугольного треугольника, если его катеты равны...
1 - Как сказочный часовой,уселся на голом суку головастый серый совенок....
2 - Придумать по на тему сила тяжести 7 класс...
1 - Напишите уравненич реакций водорода со следующими веществами o2,v2o5,ca....
2 - Катер был в пути 2: 00 проплывая 80 километров в час сколько времени...
1 - Значение пословицы: не плюй против ветра...
3
Сначала рассмотрим треугольник АВС. Поскольку АВ=BC=10, треугольник является равнобедренным.
Также известно, что А1К=KB1, поэтому треугольник А1В1К также является равнобедренным.
Поскольку А...С1 - прямая призма, высота каждого бокового треугольника в призме является перпендикуляром к основанию. Мы можем использовать это свойство, чтобы найти высоту треугольника АВС.
Из прямоугольного треугольника АВС можно найти высоту, используя теорему Пифагора: AC^2 = AB^2 + BC^2. Подставляя значения, получаем:
16^2 = 10^2 + 10^2
256 = 100 + 100
256 = 200
16 = √200
Теперь мы можем использовать высоту треугольника АВС для нахождения площади треугольника АВС.
Формула для площади треугольника: Площадь = 1/2 * основание * высота.
В данном случае, основание треугольника АВС равно 10, а высота равна √200.
Pтреугольника АВС = 1/2 * 10 * √200 = 5√200.
Теперь рассмотрим треугольник АКВ. Поскольку А1К=KB1, это также означает, что АК = КВ. Треугольник АКВ является равнобедренным.
Также известно, что в призме боковая сторона BC является высотой бокового треугольника АКВ. Она равна √200.
Теперь мы можем использовать основание АК треугольника АКВ и высоту BC, чтобы найти площадь этого треугольника.
Pтреугольника АКВ = 1/2 * АК * BC = 1/2 * 10 * √200 = 5√200.
Наконец, чтобы найти площадь сечения AKC плоскостью, мы должны сложить площади треугольников АВС и АКВ.
Pсеч. пл. AKC = Pтреугольника АВС + Pтреугольника АКВ = 5√200 + 5√200 = 10√200.
Таким образом, площадь сечения AKC плоскостью равна 10√200.