Дано: a||b, угол 1 в 4 раза меньше, чем угол 2
Найти: угол 3
Памагити
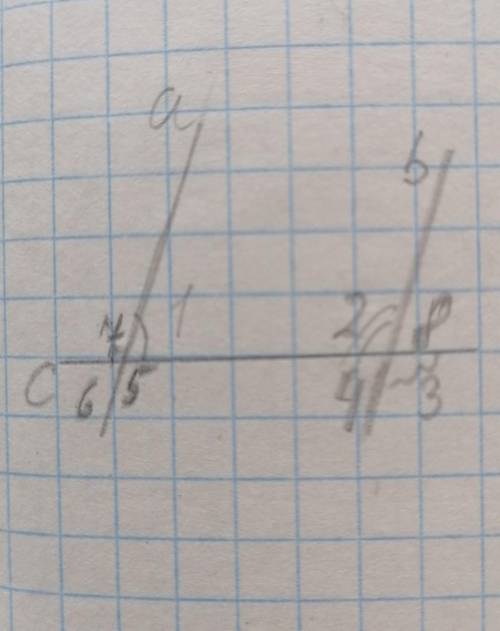
Другие вопросы по теме Геометрия
Популярные вопросы
- Бірліктерінің қосындысы 16, ал одақтарының қосындысы 7тең болатын екі таң...
3 - Какое из перечислены ниже племён не относится к германским а] лангобары...
2 - Кжевательным мышцам относится 1) височная 2грудино-ключично-сосцевидная...
3 - Турист км за три дня во второй день на восемь км меньше чем в первый и на...
2 - Как это читается на буквами my name is i am in the 7 th form i live in a...
2 - Kml=108 om-биссектриса. найдите меру oml...
3 - Кажите точку графика функции y=x^2+4x, в которой касательная параллельна...
2 - Соль об открытие вещества об отличительных особенностях( свойства и т.д.)...
2 - Учеловека кареглазость - доминантный признак. в семье из 5 человек у отца...
3 - Скакими из перечисленных веществ: а)hno3,so3,koh,feo,h2o будет реагировать...
2
У нас есть две параллельные прямые a и b, а также углы 1, 2 и 3.
Согласно условию, угол 1 в 4 раза меньше, чем угол 2. Пусть мера угла 1 равна x градусам. Тогда мера угла 2 будет равна 4x градусам.
Мы должны найти меру угла 3. Для этого воспользуемся свойством, что сумма углов треугольника равна 180 градусам.
Обратите внимание, что углы 1 и 2 образуют линейную пару с углом 3, так как прямые a и b параллельны. Значит, угол 1 + угол 2 + угол 3 = 180.
Подставим известные значения в данное уравнение:
x + 4x + угол 3 = 180
Упростим уравнение:
5x + угол 3 = 180
Теперь нам нужно выразить угол 3. Для этого вычтем 5x из обеих сторон уравнения:
угол 3 = 180 - 5x
Таким образом, мы получили выражение для меры угла 3 в терминах неизвестного x.
Но нам дано только, что угол 1 в 4 раза меньше, чем угол 2. Чтобы найти конкретные значения x и угла 3, нам понадобятся дополнительные данные. Если они есть, пожалуйста, предоставьте их, и я помогу вам окончательно решить задачу.