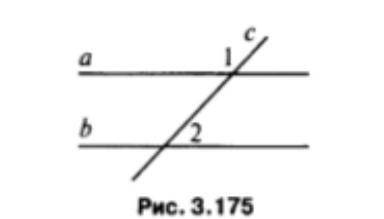
Дано: а||b, c - секущая <1:<2 = 7:2
Найти: все образовшиеся углы
даю 30б
Другие вопросы по теме Геометрия
Популярные вопросы
- Укажите при каком значении параметра a уравнения (a+1)x^2+8x+a-3=0 является неполным...
1 - Вова старше коли на 29 месяцев, но младше саши на 8640 часов.на сколько саша старше...
1 - Прочитайте. желтенький цыпленок, сероватая , , лучистый , , глиняная , кожаный...
3 - Чему равен заряд цинковой пылинки массой 10(-9 степени) г, если она находится...
1 - Свойства, свойства, получение, применение.(алкенов )...
1 - Какую цифру нужно поставить вместо звёздочки чтобы полученное число делилось на...
2 - Перевидите . вот эти предложения (на казахский язык) 1) новогодняя елка- дерево...
2 - Решить рациональные уравнения 30 1) 3/х+4=5/х+8 2)5m/12-m/8=1/3 3)4-x/12=5/x+3...
1 - Надо подобрать подходящие по смыслу глаголы и указать спряжение утюгом,плугом,жерновами,топором,глазами,ушами,ногами....
1 - Отметьте слова у которых при изменении формы в корне встречается беглый гласный...
1
Изображение показывает две параллельные прямые а и b, которые пересекаются секущей c. В задаче дано, что углы 1 и 2 образованные секущей и прямой а равны в отношении 7:2.
Подробное решение:
1) Рассмотрим углы, образованные секущей и прямой б:
а1 = 180° - угол 1 (сумма углов на прямой равна 180°)
а2 = 180° - угол 2 (сумма углов на прямой равна 180°)
2) Так как а и b – параллельные прямые, то углы а1 и а2 также равны:
а1 = а2
3) По условию а1 : а2 = 7 : 2, а значит, если найдем значение одного из этих углов, сможем найти и значение другого угла:
а1 = 7x
а2 = 2x,
где х – некое число, которое мы должны найти.
4) Также важно помнить, что сумма углов а1 и а2 равна 180°:
а1 + а2 = 180°
7x + 2x = 180°
5) При решении данного уравнения получаем:
9x = 180°
x = 20°
6) Теперь мы знаем значения углов а1 и а2:
а1 = 7x = 7 * 20° = 140°
а2 = 2x = 2 * 20° = 40°
Таким образом, все образовавшиеся углы:
а1 = 140°
а2 = 40°
1 = а1 = 140°
2 = а2 = 40°
Ответ: угол 1 равен 140°, угол 2 равен 40°, угол а1 равен 140°, угол а2 равен 40°.