Дано: а(10; -5) и в(-2; 1) - концы диаметра окружности. а) найдите координаты центра окружностиб) запишите ур-е этой окружности (в этом сложность,

Question

Геометрия: Дано: а(10; -5) и в(-2; 1) - концы диаметра окружности. а) найдите координаты центра окружностиб) запишите ур-е этой окружности (в этом сложность, ведь надо найти радиус, а чтобы найти радиус, надо найти диаметр, а как там его найти - не понимаю)в) принадлежит ли этой окружности точка d(-5; -2)? ​

бахтылбек · Answer

а) Центр окружности (точка О) является серединой отрезка АВ. Найдем координаты точки О:

$\displaystyle\tt O\bigg(\frac{10+(-2)}{2}; \ \frac{-5+1}{2}\bigg) \ \ \Rightarrow \ \ O (4; -2)$

б) Используя формулу длины отрезка, найдём длину радиуса окружности (отрезок ОА):

$\displaystyle\tt OA=\sqrt{(10-4)^2+(-5-(-2))^2}=\sqrt{36+9}=\sqrt{45} =3\sqrt{5}$

Запишем уравнение окружности:

$\displaystyle\tt (x-4)^2+(y-(-2))^2=(3\sqrt{5})^2\\ \\ (x-4)^2+(y+2)^2=45$

в) Подставим координаты точки D в уравнение окружности:

$\displaystyle\tt (x-4)^2+(y+2)^2=45\\\\ (-5-4)^2+(-2+2)^2=45\\\\ (-9)^2+0^2=45\\\\ 81\neq 45$

Точка D не принадлежит данной окружности.

------------------------------------------------------------------------------

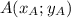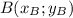P.S. Пусть даны точки A(x_A;y_A) и B(x_B;y_B) . Длину отрезка АВ вычисляем по формуле:

$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$

Популярные вопросы